Programmable NVIDIA GPUs are very inspiring to hardware geeks, proving that processors with an original, incompatible programming model can become widely used.
NVIDIA call their parallel programming model SIMT - "Single Instruction, Multiple Threads". Two other different, but related parallel programming models are SIMD - "Single Instruction, Multiple Data", and SMT - "Simultaneous Multithreading". Each model exploits a different source of parallelism:
- In SIMD, elements of short vectors are processed in parallel.
- In SMT, instructions of several threads are run in parallel.
- SIMT is somewhere in between – an interesting hybrid between vector processing and hardware threading.
My presentation of SIMT is focused on hardware architecture and its implications on the trade-off between flexibility and efficiency. I'll describe how SIMT is different from SIMD and SMT, and why – what is gained (and lost) through these differences.
From a hardware design perspective, NVIDIA GPUs are at first glance really strange. The question I'll try to answer is "why would you want to build a processor that way?" I won't attempt to write a GPU programming tutorial, or quantitatively compare GPUs to other processors.
SIMD < SIMT < SMT
It can be said that SIMT is a more flexible SIMD, and SMT is in turn a more flexible SIMT. Less flexible models are generally more efficient – except when their lack of flexibility makes them useless for the task.
So in terms of flexibility, SIMD < SIMT < SMT. In terms of performance, SIMD > SIMT > SMT, but only when the models in question are flexible enough for your workload.
SIMT vs SIMD
SIMT and SIMD both approach parallelism through broadcasting the same instruction to multiple execution units. This way, you replicate the execution units, but they all share the same fetch/decode hardware.
If so, what's the difference between "single instruction, multiple data", and single instruction, multiple threads"? In NVIDIA's model, there are 3 key features that SIMD doesn't have:
- Single instruction, multiple register sets
- Single instruction, multiple addresses
- Single instruction, multiple flow paths
We'll see how this lifts restrictions on the set of programs that are possible to parallelize, and at what cost.
Single instruction, multiple register sets
Suppose you want to add two vectors of numbers. There are many ways to spell this. C uses a loop spelling:
for(i=0;i<n;++i) a[i]=b[i]+c[i];
Matlab uses a vector spelling:
a=b+c;
SIMD uses a "short vector" spelling – the worst of both worlds. You break your data into short vectors, and your loop processes them using instructions with ugly names. An example using C intrinsic functions mapping to ARM NEON SIMD instructions:
void add(uint32_t *a, uint32_t *b, uint32_t *c, int n) {
for(int i=0; i<n; i+=4) {
//compute c[i], c[i+1], c[i+2], c[i+3]
uint32x4_t a4 = vld1q_u32(a+i);
uint32x4_t b4 = vld1q_u32(b+i);
uint32x4_t c4 = vaddq_u32(a4,b4);
vst1q_u32(c+i,c4);
}
}
SIMT uses a "scalar" spelling:
__global__ void add(float *a, float *b, float *c) {
int i = blockIdx.x * blockDim.x + threadIdx.x;
a[i]=b[i]+c[i]; //no loop!
}
The weird __global__ keyword says that add() is a GPU thread entry point. blockIdx, blockDim and threadIdx are built-in thread-local variables keeping the thread's ID. We'll see later why a thread ID isn't just a single number; however, in this example we in fact convert it to a single number, and use it as the element index.
The idea is that the CPU spawns a thread per element, and the GPU then executes those threads. Not all of the thousands or millions of threads actually run in parallel, but many do. Specifically, an NVIDIA GPU contains several largely independent processors called "Streaming Multiprocessors" (SMs), each SM hosts several "cores", and each "core" runs a thread. For instance, Fermi has up to 16 SMs with 32 cores per SM – so up to 512 threads can run in parallel.
All threads running on the cores of an SM at a given cycle are executing the same instruction – hence Single Instruction, Multiple Threads. However, each thread has its own registers, so these instructions process different data.
Benefits
"Scalar spelling", where you write the code of a single thread using standard arithmetic operators, is arguably a better interface than SIMD loops with ugly assembly-like opcodes.
Syntax considerations aside, is this spelling more expressive – can it do things SIMD can't? Not by itself, but it dovetails nicely with other features that do make SIMT more expressive. We'll discuss those features shortly; in theory, they could be bolted on the SIMD model, but they never are.
Costs
From a hardware resources perspective, there are two costs to the SIMT way:
- Registers spent to keep redundant data items.
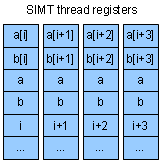In our example, the pointers a, b, and c have the same value in all threads. The values of i are different across threads, but in a trivial way – for instance, 128, 129, 130… In SIMD, a, b, and c would be kept once in “scalar” registers – only short vectors such as a[i:i+4] would be kept in “vector” registers. The index i would also be kept once – several neighbor elements starting from i would be accessed without actually computing i+1, i+2, etc. Redundant computations both waste registers and needlessly consume power. Note, however, that a combination of compiler & hardware optimizations could eliminate the physical replication of redundant values. I don't know the extent to which it's done in reality. - Narrow data types are as costly as wide data types.
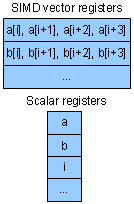A SIMD vector register keeping 4 32b integers can typically also be used to keep 8 16b integers, or 16 8b ones. Similarly, the same ALU hardware can be used for many narrow additions or fewer wide ones – so 16 byte pairs can be added in one cycle, or 4 32b integer pairs. In SIMT, a thread adds two items at a time, no matter what their width, wasting register bits and ALU circuitry.
It should be noted that SIMT can be easily amended with SIMD extensions for narrow types, so that each thread processes 4 bytes at a time using ugly assembly-like opcodes. AFAIK, NVIDIA refrains from this, presumably assuming that the ugliness is not worth the gain, with 32b float being the most popular data type in graphics anyway.
Single instruction, multiple addresses
Let's apply a function approximated by a look-up table to the elements of a vector:
__global__ void apply(short* a, short* b, short* lut) {
int i = blockIdx.x * blockDim.x + threadIdx.x;
a[i] = lut[b[i]]; //indirect memory access
}
Here, i is again "redundant" in the sense that in parallel threads, the values of i are consecutive. However, each thread then accesses the address lut+b[i] – and these addresses are not consecutive.
Roughly, such parallel random access works for both loads and stores. Logically, stores are the trickier part because of conflicts. What if two or more threads attempt to, say, increment the same bin in a histogram? Different NVIDIA GPU generations provide different solutions that we won't dwell on.
Benefits
This feature lets you parallelize many programs you can't with SIMD. Some form of parallel random access is usually available on SIMD machines under the names "permutation", "shuffling", "table look-up", etc. However, it always works with registers, not with memory, so it's just not the same scale. You index into a table of 8, 16 or 32 elements, but not 16K.
As previously mentioned, in theory this feature can be bolted on the SIMD model: just compute your addresses (say, lut+b[i]) in vector registers, and add a rand_vec_load instruction. However, such an instruction would have a fairly high latency. As we'll see, the SIMT model naturally absorbs high latencies without hurting throughput; SIMD much less so.
Costs
GPU has many kinds of memory: external DRAM, L2 cache, texture memory, constant memory, shared memory… We'll discuss the cost of random access in the context of two memories "at the extremes": DRAM and shared memory. DRAM is the farthest from the GPU cores, sitting outside the chip. Shared memory is the closest to the cores – it's local to an SM, and the cores of an SM can use it to share results with each other, or for their own temporary data.
- With DRAM memory, random access is never efficient. In fact, the GPU hardware looks at all memory addresses that the running threads want to access at a given cycle, and attempts to coalesce them into a single DRAM access – in case they are not random. Effectively the contiguous range from i to i+#threads is reverse-engineered from the explicitly computed i,i+1,i+2… – another cost of replicating the index in the first place. If the indexes are in fact random and can not be coalesced, the performance loss depends on "the degree of randomness". This loss results from the DRAM architecture quite directly, the GPU being unable to do much about it – similarly to any other processor.
- With shared memory, random access is slowed down by bank contentions. Generally, a hardware memory module will only service one access at a time. So shared memory is organized in independent banks; the number of banks for NVIDIA GPUs is 16. If x is a variable in shared memory, then it resides in bank number (&x/4)%16. In other words, if you traverse an array, the bank you hit changes every 4 bytes. Access throughput peaks if all addresses are in different banks – hardware contention detection logic always costs latency, but only actual contentions cost throughput. If there's a bank hosting 2 of the addresses, the throughput is 1/2 of the peak; if there's a bank pointed by 3 addresses, the throughput is 1/3 of the peak, etc., the worst slowdown being 1/16.
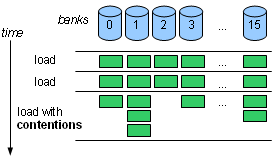
In theory, different mappings between banks and addresses are possible, each with its own shortcomings. For instance, with NVIDIA's mapping, accessing a contiguous array of floats gives peak throughput, but a contiguous array of bytes gives 1/4 of the throughput (since banks change every 4 bytes). Many of the GPU programming tricks aim at avoiding contentions.
For instance, with a byte array, you can frequently work with bytes at distance 4 from each other at every given step. Instead of accessing a[i] in your code, you access a[i*4], a[i*4+1], a[i*4+2] and a[i*4+3] – more code, but less contentions.
This sounds convoluted, but it's a relatively cheap way for the hardware to provide efficient random access. It also supports some very complicated access patterns with good average efficiency – by handling the frequent case of few contentions quickly, and the infrequent case of many contentions correctly.
Single instruction, multiple flow paths
Let's find the indexes of non-zero elements in a vector. This time, each thread will work on several elements instead of just one:
__global__ void find(int* vec, int len,
int* ind, int* nfound,
int nthreads) {
int tid = blockIdx.x * blockDim.x + threadIdx.x;
int last = 0;
int* myind = ind + tid*len;
for(int i=tid; i<len; i+=nthreads) {
if(vec[i]) { //flow divergence
myind[last] = i;
last++;
}
}
nfound[tid] = last;
}
Each thread processes len/nthreads elements, starting at the index equal to its ID with a step of nthreads. We could make each thread responsible for a more natural contiguous range using a step of 1. The way we did it is better in that accesses to vec[i] by concurrent threads address neighbor elements, so we get coalescing.
The interesting bit is if(vec[i]) – depending on vec[i], some threads execute the code saving the index, some don't. The control flow of different threads can thus diverge.
Benefits
Support for divergence further expands the set of parallelizable programs, especially when used together with parallel random access. SIMD has some support for conditional execution though vector "select" operations: select(flag,a,b) = if flag then a else b. However, select can't be used to suppress updates to values – the way myind[last] is never written by threads where vec[i] is 0.
SIMD instructions such as stores could be extended to suppress updates based on a boolean vector register. For this to be really useful, the machine probably also needs parallel random access (for instance, the find() example wouldn't work otherwise). Unless what seems like an unrealistically smart compiler arrives, this also gets more and more ugly, whereas the SIMT spelling remains clean and natural.
Costs
- Only one flow path is executed at a time, and threads not running it must wait.
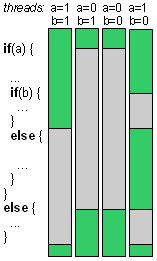Ultimately SIMT executes a single instruction in all the multiple threads it runs – threads share program memory and fetch / decode / execute logic. When the threads have the same flow – all run the if, nobody runs the else, for example – then they just all run the code in if at full throughput. However, when one or more threads have to run the else, they'll wait for the if threads. When the if threads are done, they'll in turn wait for the else threads. Divergence is handled correctly, but slowly. Deeply nested control structures effectively serialize execution and are not recommended. - Divergence can further slow things down through "randomizing" memory access. In our example, all threads read vec[i], and the indexing is tweaked to avoid contentions. However, when myind[last] is written, different threads will have incremented the last counter a different number of times, depending on the flow. This might lead to contentions which also serialize execution to some extent. Whether the whole parallelization exercise is worth the trouble depends on the flow of the algorithm as well as the input data.
We've seen the differences between SIMT and its less flexible relative, SIMD. We'll now compare SIMT to SMT – the other related model, this time the more flexible one.
SIMT vs SMT
SIMT and SMT both use threads as a way to improve throughput despite high latencies. The problem they tackle is that any single thread can get stalled running a high-latency instruction. This leaves the processor with idle execution hardware.
One way around this is switching to another thread – which (hopefully) has an instruction ready to be executed – and then switch back. For this to work, context switching has to be instantaneous. To achieve that, you replicate register files so that each thread has its own registers, and they all share the same execution hardware.
But wait, doesn't SIMT already replicate registers, as a way to have a single instruction operate on different data items? It does – here, we're talking about a "second dimension" of register replication:
- Several threads – a "warp" in NVIDIA terminology – run simultaneously. So each thread needs its own registers.
- Several warps, making up a "block", are mapped to an SM, and an SM instantaneously switches between the warps of a block. So each warp needs separate registers for each of its threads.
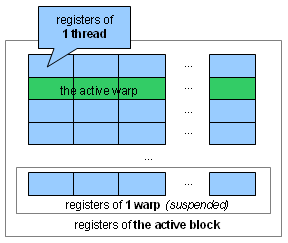
With this "two-dimensional" replication, how many registers we end up with? Well, a lot. A block can have up to 512 threads. And the registers of those threads can keep up to 16K of data.
How many register sets does a typical SMT processor have? Er, 2, sometimes 4…
Why so few? One reason is diminishing returns. When you replicate registers, you pay a significant price, in the hope of being able to better occupy your execution hardware. However, with every thread you add, the chance of it being already occupied by all the other threads rises. Soon, the small throughput gain just isn't worth the price.
If SMT CPU designers stop at 2 or 4 threads, why did SIMT GPU designers go for 512?
With enough threads, high throughput is easy
SMT is an afterthought – an attempt to use idle time on a machine originally designed to not have a lot of idle time to begin with. The basic CPU design aims, first and foremost, to run a single thread fast. Splitting a process to several independent threads is not always possible. When it is possible, it's usually gnarly.
Even in server workloads, where there's naturally a lot of independent processing, single-threaded latency still matters. So few expensive, low-latency cores outperform many cheap, high-latency cores. As Google's Urs Hölzle put it, "brawny cores beat wimpy cores". Serial code has to run fast.
Running a single thread fast means being able to issue instructions from the current thread as often as possible. To do that, CPU hardware works around every one of the many reasons to wait. Such diverse techniques as:
- superscalar execution
- out-of-order execution
- register renaming
- branch prediction
- speculative execution
- cache hierarchy
- speculative prefetching
- etc. etc.
…are all there for the same basic purpose. They maximize the chances of an instruction to be issued without having to switch to another thread.
SMT is the last line of defense, attempting to fill stalls after all these other measures failed. And even that is considered a bad idea when it hurts the precious single-threaded performance. Which it usually does: each of the 2 threads will typically complete later then it would if it didn't have to share the hardware with the other. This is a key reason to keep the number of hardware threads low, even if there are still throughput gains to be made by adding threads.
However, for the GPUs, the use case is when you do have enough data parallelism to make use of plenty of threads. If so, why not build things the other way around? Threading could be our first stall-mitigating measure. If we have enough threads, we just keep switching between them, and the hardware always has something to do.
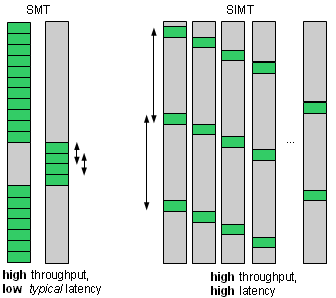
This saves a lot of hardware, and a lot of design effort, because you don't need most of the other methods anymore. Even caches and hardware prefetching are not used in much of the GPU memory traffic – rather, you access external memory directly. Why bother with caching and prefetching, if you don't have to sit idly until the data arrives from main memory – but instead just switch to a different warp? No heuristics, no speculation, no hurry – just keep yourself busy when waiting.
Furthermore, even the basic arithmetic pipeline is designed for a high latency, high throughput scenario. According to the paper "Demystifying GPU architecture through microbenchmarking", no operation takes less than 24 cycles to complete. However, the throughput of many operations is single-cycle.
The upshot is that counting on the availability of many threads allows the GPU to sustain a high throughput without having to sweat for low latencies. Hardware becomes simpler and cheaper in many areas as a result.
When latencies are high, registers are cheap
So plentiful threads make it easier to build high-throughput hardware. What about having to replicate all those registers though? 16K sounds like an insane amount of registers – how is this even affordable?
Well, it depends on what "register" means. The original meaning is the kind of storage with the smallest access latency. In CPUs, access to registers is faster than access to L1 caches, which in turn is faster than L2, etc. Small access latency means an expensive implementation, therefore there must be few registers.
However, in GPUs, access to "registers" can be quite slow. Because the GPU is always switching between warps, many cycles pass between two subsequent instructions of one warp. The reason registers must be fast in CPUs is because subsequent instructions communicate through them. In GPUs, they also communicate through registers – but the higher latency means there's no rush.
Therefore, GPU registers are only analogous to CPU registers in terms of instruction encoding. In machine code, "registers" are a small set of temporary variables that can be referenced with just a few bits of encoding – unlike memory, where you need a longer address to refer to a variable. In this and other ways, "registers" and "memory" are semantically different elements of encoding – both on CPUs and GPUs.
However, in terms of hardware implementation, GPU registers are actually more like memory than CPU registers. [Disclaimer: NVIDIA doesn't disclose implementation details, and I'm grossly oversimplifying, ignoring things like data forwarding, multiple access ports, and synthesizable vs custom design]. 16K of local RAM is a perfectly affordable amount. So while in a CPU, registers have to be expensive, they can be cheap in a high-latency, high-throughput design.
It's still a waste if 512 threads keep the same values in some of their registers – such as array base pointers in our examples above. However, many of the registers keep different values in different threads. In many cases register replication is not a waste at all – any processor would have to keep those values somewhere. So functionally, the plentiful GPU registers can be seen as a sort of a data cache.
Drawbacks
We've seen that:
- Many threads enable cheap high-throughput, high-latency design
- A high-throughput, high-latency design in turn enables a cheap implementation of threads' registers
This leads to a surprising conclusion that SIMT with its massive threading can actually be cheaper than SMT-style threading added to a classic CPU design. Not unexpectedly, these cost savings come at a price of reduced flexibility:
- Low occupancy greatly reduces performance
- Flow divergence greatly reduces performance
- Synchronization options are very limited
Occupancy
"Occupancy" is NVIDIA's term for the utilization of threading. The more threads an SM runs, the higher its occupancy. Low occupancy obviously leads to low performance – without enough warps to switch between, the GPU won't be able to hide its high latencies. The whole point of massive threading is refusing to target anything but massively parallel workloads. SMT requires much less parallelism to be efficient.
Divergence
We've seen that flow divergence is handled correctly, but inefficiently in SIMT. SMT doesn't have this problem – it works quite well given unrelated threads with unrelated control flow.
There are two reasons why unrelated threads can't work well with SIMT:
- SIMD-style instruction broadcasting – unrelated threads within a warp can't run fast.
- More massive threading than SMT – unrelated wraps would compete for shared resources such as instruction cache space. SMT also has this problem, but it's tolerable when you have few threads.
So both of SIMT's key ideas – SIMD-style instruction broadcasting and SMT-style massive threading – are incompatible with unrelated threads.
Related threads – those sharing code and some of the data – could work well with massive threading by itself despite divergence. It's instruction broadcasting that they fail to utilize, leaving execution hardware in idle state.
However, it seems that much of the time, related threads actually tend to have the same flow and no divergence. If this is true, a machine with massive threading but without instruction broadcasting would miss a lot of opportunities to execute its workload more efficiently.
Synchronization
In terms of programming model, SMT is an extension to a single-threaded, time-shared CPU. The same fairly rich set of inter-thread (and inter-device) synchronization and communication options is available with SMT as with "classic" single-threaded CPUs. This includes interrupts, message queues, events, semaphores, blocking and non-blocking system calls, etc. The underlying assumptions are:
- There are quite many threads
- Typically, each thread is doing something quite different from other threads
- At any moment, most threads are waiting for an event, and a small subset can actually run
SMT stays within this basic time-sharing framework, adding an option to have more than one actually running threads. With SMT, as with a "classic" CPU, a thread will be very typically put "on hold" in order to wait for an event. This is implemented using context switching – saving registers to memory and, if a ready thread is found, restoring its registers from memory so that it can run.
SIMT doesn't like to put threads on hold, for several reasons:
- Typically, there are many running, related threads. It would make the most sense to put them all on hold, so that another, unrelated, equally large group of threads can run. However, switching 16K of context is not affordable. In this sense, "registers" are expensive after all, even if they are actually memory.
- SIMT performance depends greatly on there being many running threads. There's no point in supporting the case where most threads are waiting, because SIMT wouldn't run such workloads very well anyway. From the use case angle, a lot of waiting threads arise in "system"/"controller" kind of software, where threads wait for files, sockets, etc. SIMT is purely computational hardware that doesn't support such OS services. So the situation is both awkward for SIMT and shouldn't happen in its target workloads anyway.
- Roughly, SIMT supports data parallelism – same code, different data. Data parallelism usually doesn't need complicated synchronization – all threads have to synchronize once a processing stage is done, and otherwise, they're independent. What requires complicated synchronization, where some threads run and some are put on hold due to data dependencies, is task parallelism – different code, different data. However, task parallelism implies divergence, and SIMT isn't good at that anyway – so why bother with complicated synchronization?
Therefore, SIMT roughly supports just one synchronization primitive – __syncthreads(). This creates a synchronization point for all the threads of a block. You know that if a thread runs code past this point, no thread runs code before this point. This way, threads can safely share results with each other. For instance, with matrix multiplication:
- Each thread, based on its ID – x,y – reads 2 elements, A(x,y) and B(x,y), from external memory to the on-chip shared memory. (Of course large A and B won't fit into shared memory, so this will be done block-wise.)
- Threads sync – all threads can now safely access all of A and B.
- Each thread, depending on the ID, multiplies row y in A by column x in B.
//1. load A(x,y) and B(x,y) int x = threadIdx.x; int y = threadIdx.y; A[stride*y + x] = extA[ext_stride*y + x]; B[stride*y + x] = extB[ext_stride*y + x]; //2. sync __syncthreads(); //3. multiply row y in A by column x in B float prod = 0; for(int i=0; i<N; ++i) { prod += A[stride*y + i] * B[stride*i + x]; }
It's an incomplete example (we look at just one block and ignore blockIdx, among other thing), but it shows the point of syncing – and the point of these weird "multi-dimensional" thread IDs (IDs are x,y,z coordinates rather than just integers). It's just natural, with 2D and 3D arrays, to map threads and blocks to coordinates and sub-ranges of these arrays.
Summary of differences between SIMD, SIMT and SMT
SIMT is more flexible in SIMD in three areas:
- Single instruction, multiple register sets
- Single instruction, multiple addresses
- Single instruction, multiple flow paths
SIMT is less flexible than SMT in three areas:
- Low occupancy greatly reduces performance
- Flow divergence greatly reduces performance
- Synchronization options are very limited
The effect of flexibility on costs was discussed above. A wise programmer probably doesn't care about these costs – rather, he uses the most flexible (and easily accessible) device until he runs out of cycles, then moves on to utilize the next most flexible device. Costs are just a limit on how flexible a device that is available in a given situation can be.
"SIMT" should catch on
It's a beautiful idea, questioning many of the usual assumptions about hardware design, and arriving at an internally consistent answer with the different parts naturally complementing each other.
I don't know the history well enough to tell which parts are innovations by NVIDIA and which are borrowed from previous designs. However, I believe the term SIMT was coined by NVIDIA, and perhaps it's a shame that it (apparently) didn't catch, because the architecture "deserves a name" – not necessarily true of every "new paradigm" announced by marketing.
One person who took note is Andy Glew, one of Intel's P6 architects – in his awesome computer architecture wiki, as well as in his presentation regarding further development of the SIMT model.
The presentation talks about neat optimizations – "rejiggering threads", per-thread loop buffers/time pipelining – and generally praises SIMT superiority over SIMD. Some things I disagree with – such as the "vector lane crossing" issue – and some are very interesting, such as everything about improving utilization of divergent threads.
I think the presentation should be understandable after reading my oversimplified overview – and will show where my overview oversimplifies, among other things.
Peddling fairness
Throughout this overview, there's this recurring "fairness" idea: you can trade flexibility for performance, and you can choose your trade-off.
It makes for a good narrative, but I don't necessarily believe it. You might very well be able to get both flexibility and performance. More generally, you might get both A and B, where A vs B intuitively feels like "an inherent trade-off".
What you can't do is get A and B in a reasonably simple, straightforward way. This means that you can trade simplicity for almost everything – though you don't necessarily want to; perhaps it's a good subject for a separate post.
511 comments ↓
Great article as always. Thanks a bunch!
Glad you liked it.
This is a really nice writeup; I think it explains a lot of the details of this stuff very well. A few comments/thoughts..
First, to argue a detail, toward the end you make the connection between SIMT and massive numbers of threads to hide latency. I think that these two things are actually orthogonal; one could build a SIMD processor that also did the same trick for latency hiding, for example. It so happens that NV's SIMT processors today hide latency with many threads, but strictly speaking I think the two things are basically independent.
Another general issue is that one can provide a SIMT model to the user on a variety of underlying h/w architectures. For example, the ispc compiler (http://ispc.github.com) provides a ~SIMT model on the CPU (that turns out to be a really good way to use the CPU's vector units). In that case, there is more work to do in the compiler and generated code to deal with control flow divergence, doing scatters/gathers to memory efficiently, etc., but in the end, it's just a different set of trade-offs of what's done in the hardware and what's done by the compiler.
(One nice thing about SIMT on the CPU is that some of the issues you mention about redundant storage of data items with the same value aren't a problem there–ispc for example provides a 'uniform' data type qualifier that indicates that a variable has the same value for all of the SIMD lanes, which directly addresses the issue you bring up here.)
From what I've seen of AMD's GPU ISA, they are at a middle ground between today's CPUs and NV's GPUs in this respect, where their documented ISA has some SIMD-isms and some SIMT-isms, but the compiler seems to do more work to make everything work than is needed on NV GPUs.
@Matt: thanks; my knowledge of the subject is comparatively scarce, glad to know the thing made sense to you.
Regarding a processor hiding latency using an SIMD model – you mean plenty of SIMD threads instead of plenty of warps, or a single thread with logically very wide SIMD instructions that take multiple stages to execute physically, or something else? Anyway, one thing regarding this write-up is that it more or less ignores the difference between interface and implementation – basically the assumption is that the execution model is implemented relatively straightforwardly.
Similarly, providing a SIMT interface on a SIMD CPU seems very hard, on two levels – the compiler back-end work and the programmer's ability to predict the extent of optimization his code will undergo (though without doubt the portability and readability of the code compared to hand-optimizing using intrinsics is a great benefit).
On reason I ignore the possibility of doing such a thing is because I personally lack the resources – including cranial horsepower – to do it, or at least to count on being able to do it well before I invested a lot of effort into trying. So when I think about processor features I'd like to implement, I evaluate them based on a straightforward usage model and not a sophisticated usage model – for SIMD, that'd be intrinsics and not SPMD code.
In this light, as well as in the more general context of hardware-software co-evolution – one thing that would be really interesting to hear is if you have suggestions for extending the SIMD model in ways making SPMD compilation more straightforward, or possible in more cases. I'd assume there would be much rejoicing if SIMD could be reliably targeted by portable, readable SPMD code some day in the future, and I'd assume hardware could help.
Regarding the "uniform" qualifier – interesting that you have that; I guess it indicates that it's valuable in the sense that it's not necessarily trivially recoverable info for the compiler and/or programmer based on the program flow. As to CPU vs GPU – I wonder how much optimization happens there in order to keep redundant values once, or at least #threads-in-warp times and not #threads-in-block times.
From the ISPC manual:
The code generated for 8 and 16-bit integer types is generally not as efficient as the code generated for 32-bit integer types. It is generally worthwhile to use 32-bit integer types for intermediate computations, even if the final result will be stored in a smaller integer type.
…this is similar to the situation with NVIDIA GPUs, where using narrow types doesn't buy you performance. This might not be a problem for graphics or scientific computing code, but it's a major problem for image processing/computer vision code, and it's inherently wasteful at the hardware level (adding 4 pairs of bytes is as cheap or cheaper than adding 2 32b integer, multiplying 2 integers is actually ~4x more expensive in terms of circuitry than multiplying 4 pairs of bytes). I don't quite see how SIMT/SPMD can handle this problem apart from re-introducing intrinsics (single SIMD instruction, multiple threads – SIMD SIMT or SSIMDIMT).
Hi, Yossi–
Regarding latency hiding, I'm just saying that any HW architecture, be it a conventional CPU or a modern GPU can use the trick of "have 8-16 of HW threads and be able to switch between them with very little overhead" to hide off-chip memory latency. No CPU today does that (and I'm not sure if it makes sense to do that on the CPU in general), but the point is just that I argue that latency hiding isn't a characteristic of the SIMT model per se.
One other small comment I forgot in my first reply regarding "SIMD instructions such as stores could be extended to suppress updates based on a boolean vector register": the latest versions of the AVX instruction set have masked load and masked store instructions that do just this.
Regarding "Similarly, providing a SIMT interface on a SIMD CPU seems very hard, on two levels – the compiler back-end work and the programmer’s ability to predict the extent of optimization his code will undergo (though without doubt the portability and readability of the code compared to hand-optimizing using intrinsics is a great benefit)."
The ispc compiler does this already–check it out! It is a decent amount of code to implement, but on the other hand, it is implementable. The question about how well the programmer can reason about the code is a good one. One thing that I do think is good about SIMT/SPMD on all types of processors (both CPU and GPU) is that the main things to reason about for performance are control flow convergence/divergence and memory access convergence/divergence.
The performance characteristics of the control flow part are similar on both CPU and GPU–the more converged the better, but there's a smooth perf. fall-off as it diverges more. Memory is more tricky: on the GPU, one benefits based on how coherent/coalesced memory accesses are at runtime, whereas on CPU (until there are gather and scatter instructions), it depends on what the compiler can figure out at compile-time. In general of course, there are lots of cases where memory locations accessed are data-dependent and thus can't be reasoned about at compile time. But on the other hand, it's surprising how efficient well-coded scatters and gathers are on the CPU, even without those available as native instructions.
> "In this light, as well as in the more general context of hardware-software co-evolution – one thing that would be really interesting to hear is if you have suggestions for extending the SIMD model in ways making SPMD compilation more straightforward, or possible in more cases. "
It's always possible, it's just a question of how many instructions it takes to do a particular operaion. :-). In general, I've been surprised at how efficiently CPU SIMD instructions can run SPMD code, even if not originally designed for it. New features like the masked loads and stores in AVX (and the gather instruction coming in AVX2) help with this a lot as well.
I understood that ispc already did this – that is, that you already did this :) Regarding ispc, I'm very curious about two things:
1. Its model is less explicit than intrinsics, but more explicit than auto-vectorization. How far is it from auto-vectorization – what work do auto-vectorizers have to do that ispc doesn't already do?
2. Is there a plan for ports to non-Intel SIMD architectures? (It's an open project, so perhaps someone outside Intel figured they'd want such a port?)
Regarding the hardware features that could be helpful for SPMD – so it's mostly masked side effects and scatter/gather? Is there anything that you'd like done to make operations working on narrow types (8b, 16b) more usable?
(The two problems that come to mind with narrow types are that the number of operands processed in parallel varies with the operand width, which doesn't trivially fit into the SPMD one-operation-per-lane model – not sure how hardware could help here; and that the C type promotion rules can be inconsistent with the input/output types of narrow-type SIMD operations – perhaps here, adapting hardware features and language features to meet somewhere in the middle could help?)
Regarding a latency-hiding non-SIMT architecture – one could make a heavily multi-threaded SIMD machine, though it would be more of a GPU than a CPU in the sense of not supporting single-threaded workloads or many unrelated threads very well. I agree that massive threading is a feature of the SIMT model conceptually separate from its other features, it just seems to be useful in about the same situations as its other features.
The narrower types are tricky; to be honest I haven't thought carefully about them. I do believe that it's important to support them well–the issues you bring up above are good ones.
The way I'd compare/contrast to auto-vectorization is that an auto-vectorizer has to take serial code and prove to itself that the code can be run in parallel (no loop-carried dependencies, etc.) This is tricky in practice for a few reasons. First, many auto-vectorizers aren't able to handle complex data-dependent control flow inside the loops–i.e. if you're looping over an array of values and then have a while() loop inside your for() loop that does a number of iterations based on the value loaded from the array. This is "just" an implementation issue, though.
The bigger issue is that there are many cases where an auto-vectorizer just can't prove loop iteration independence–consider calling a function within a loop that was defined in another source file. The compiler has no visibility into what that function will do, so it has to assume the worst case and not auto-vectorize.
Conversely, a SPMD/SIMT/whatever compiler has a fundamentally parallel execution model; the programmer is implicitly promising the compiler that it's safe to run multiple instances of the program in parallel (across vector lanes and or cores)–either because there are no dependencies between program instances, or because appropriate synchronization calls have been added to the code. Thus the compiler doesn't have to worry about proving independence at all–it just goes parallel and doesn't worry about it.
For legacy code and for programmers who are willing to trade-off performance for safety, auto-vectorizing technology is great. But I think that there is a class of highly performance-oriented programmers (people who program GPUs today, write intrinsics by hand, etc.), who are quite happy to make that guarantee to the compiler in exchange for guaranteed good utilization of the SIMD unit…
This is interesting and admittedly unexpected to me – if I understand correctly, you're saying that the biggest trouble of an auto-vectorizer is proving that its use would preserve the semantics of the code, right?
If so, and supposing we're targeting people who're willing to tweak code for performance and to stray from standard C, but who also generally prefer to keep as much of the code as close to the standard as possible – couldn't something like #pragma independent_iterations in front of a loop be sufficient?
One way in which this would seem to be insufficient to me is things like vector shuffling – in ispc, "inter-lane cross-talk" is handled with the intrinsic-like calls such as broadcast() and shuffle(), which works because the code is basically spelled so that work is explicitly distributed across lanes, so code can meaningfully refer to these lanes. If the code used a "normal" loop and incremented the index by a single step and not by #lanes steps every time, shuffling would become a sort of inter-iteration dependence – and the auto-vectorizer would have to deal with it.
Is this the kind of thing that makes something along the lines of #pragma trust_me a not good enough way to make auto-vectorization practical – or would you label that case with "non-fundamental", "just" implementation issues?
(If the single fundamental issue is data and control flow analysis, I'd expect reasonable performance-aware programmers to be very willing to add restrict to every pointer they pass to kernel code, and to make sure kernel code never relies on separate compilation and function pointers – which presumably makes flow analysis feasible; if the unwillingness of people to do this is the only truly insurmountable obstacle to the adoption of auto-vectorizers, it's very surprising.)
In the context of CUDA, SM is streaming multiprocessor, not streaming module.
Thanks! Fixed.
I wasn't aware of the 4-byte distribution of shared memory. Do you have an Nvidia source to cite for that? I implemented it and did see a speed-up, but I'd like to be able to cite it.
One place it's mentioned is NVIDIA CUDA Programming Guide, page 90: "In the case of the shared memory space, the banks are organized such that
successive 32-bit words are assigned to successive banks and each bank has a
bandwidth of 32 bits per two clock cycles." … "there are bank conflicts if an array
of char is accessed the following way:
__shared__ char shared[32];
char data = shared[BaseIndex + tid];
because shared[0], shared[1], shared[2], and shared[3], for example,
belong to the same bank. There are no bank conflicts however, if the same array is
accessed the following way:
char data = shared[BaseIndex + 4 * tid];"
(They also mention the special case of broadcasting – when N threads access the same address in the same bank, the broadcasting of the single accessed value to them all is handled efficiently and does not cause slowdown. I decided to not mention this special case for brevity, though perhaps it is important to support in hardware for getting straightforwardly written programs to run fast.)
In my particular scenario, I have four 1-byte fields per thread, originally in four separate arrays (e.g., field_a[], field_b[], field_c[], field_d[]). This is obviously bad because the threads would hit the same bank of memory in groups of four. I changed my implementation to something like you describe:
__shared__ char thread_data[THREADS_PER_BLOCK * 4];
char field_a = thread_data[4 * threadIdx.x + 0];
char field_b = thread_data[4 * threadIdx.x + 1];
char field_c = thread_data[4 * threadIdx.x + 2];
char field_d = thread_data[4 * threadIdx.x + 3];
This definitely improved my memory access pattern, effectively giving each thread (in groups of 16, of course) it's own bank of memory. I don't think I can improve it any further at this point.
Unfortunately, while implementing this I happened to notice a place where I wasn't freeing a significant block of memory (oops!). This is good, since I'd been have issues with large data sets, but it tacked on a ms or two to my cycle time so I can no longer claim this optimization gave me a 20% speed boost ;)
Thanks for the reference as well as the article, I enjoyed reading it.
Also, it seems that the latest version of the Programming Guide (http://developer.download.nvidia.com/compute/DevZone/docs/html/C/doc/CUDA_C_Programming_Guide.pdf) has more information about shared memory conflicts in section F.3.3.
Glad to have helped; I have to say that my own hands-on experience with CUDA is minimal…
I really liked the post, was a great introduction to SIMT to me.
Also I found it cool (if maybe not totally surprising) that the meta-lesson "you can trade simplicity for almost anything" reappears in this context as well. The same is definitely true for the area I'm working on, which is VMs for (dynamic) languages.
Glad you liked it! As to "simplicity for almost anything" (sounds like VMs are the classic example) – actually, it's an interesting question how applicable it is to hardware design, because one thing that you usually lose with simplicity is size. In hardware, code size translates to hardware size – but not straightforwardly, that is, some things can be very complicated in code but not very large; and then size translates to power consumption, but also not straightforwardly.
I never really explored this with hardware, in the sense that I try to stay away from complexity in that area as much as possible, mainly to avoid bugs but also to have performance characteristics that are humanly comprehensible. If we look at CPUs (a kind of hardware that rewards complexity more than other kinds), we'll see that, on the one hand, the very complicated x86 designs are losing in the mobile space because ultimately that complexity does translate to too much area & power consumption; but on the other hand, embedded CPUs – ARM, MIPS, etc. – are moving towards super-scalar, hyper-threaded designs, which are far from the most straightforward CPU design.
In one way, CPUs are not unlike VMs (on different levels, they both try to efficiently run programs by applying non-straightforward analysis – typically without having the luxury of forcing the program authors to apply this analysis themselves and spell programs such that it's obvious how to run them efficiently) – so it seems that both spaces would reward complexity to some extent. I do believe that accelerator hardware like GPUs or DSPs is more "complexity-hostile" in the sense that due to price/performance considerations, it's a better idea to push much of the complexity onto software and move it out of the hardware.
Nice article. Your comment re complexity. The research shows that SIMT can indeed produce good utilisation of hardware resources. However, those of us who are in the thick of maximising performance vs energy realise that you must increase the bang per memory operation if you are to increase the power efficiency. SIMT starts to get a little harder when you consider more computational depth in the pipelines. Also modern SIMT needs to be generalised, not just for graphics and both the power efficiency and generality will move SIMT into more complexity, particularly in the numbers of sequencial instructions that need to skip references to the register file.
…Because the register file is actually memory and you'd like more bang per memory operation, I guess. Great point.
As to utilization research – it ought to depend a great deal on your workload; for instance, SIMT is a terrible idea for most of my workloads simply because there's no way to sensibly spawn and occupy that many threads cooperating the way SIMT threads do.
Indeed. However, even partial system utilisation (good single block utilisation) may mean substantial power savings over a CPU + SIMD, as long as the SoC has good partial powerdown or clock gating.
Block – you mean a single "SM" in NVIDIA-speak, or a single "core"? I'm guessing SM – if so, keeping an SM occupied is already challenging for many workloads – 16/32 threads times latency of 28 translates to ~500-900 threads to keep an SM busy (I think these are realistic numbers).
Nice article! I've never read about this nor CUDA, but have studied about SIMD, so I could understand this :D
Thx. For weeks I had this article open and finally found the time to read it. It was definitly worth the time :-)
Thanks!
I think you are confusing people by conflating SIMD and SWAR (SIMD Within A Register). Having a program counter (PC) per core and other features is still fundamentally SIMD. AMD calls their Graphics Core Next technology SIMD and they have an 80 bit PC per core.
You're technically correct, however, SIMD is most often used to mean "SIMD within a register", and SWAR is almost never used.
I come with a background in SIMD and this is easily the best article I've read that comprehensively covers GPU architecture details in an intuitive manner. Thank you so much Yossi!
Glad you liked it!
Thanks for this article. I've been trying to figure out whether my genetic algorithm categorising code can be shoehorned into a SIMD/SIMT type structure (say on a Kepler K1 board), or whether it really needs multiple independent cores (eg Parallella 16 core, or a small cluster of ARM 4/8 core boards). Still undecided, but your article has certainly encouraged me to explore this further.
Hi Yossi. This is a good article to distinguish SIMD, SMT, and SIMT. I am confused about SIMD or MIMD. Are they computer architecture or programming model? It seems that the architecture and programming model can be mixed. Do you have any books or papers which can well explain these?
As you obtain more adept at using magic, you will have to learn how to cope with runes.
This is probably not familiar with secure the validity associated
with progression of thoughts due to the inescapable fact it absolutely was your head itself that set the footwork for that theory.
This flying series flight simulator in Canada
is one strategy to experience the best way to chance a plane and
visit various areas of the world.
Hi to every body, it's my first visit of this weblog; this blog includes remarkable and actually excellent material in support of visitors.
Therefore, it is important to restore this error with your Pc since
although it gets risky, all those unseen process
computer file are able to use up the stored data slowly.
Working inside a state-of-the-art lab, these experts concentrate on conducting persistent and thorough research, to make certain their methods stop at the
very forefront of digital and computer forensics. Furthermore, all this handles those
Windows xp dll computer files and hang down them into Microsoft windows memory.
Hello, I enjoy reading through your article post. I like to write a little
comment to support you.
naturally like your web-site but you have to take a look at the spelling on quite a few of your posts.
Several of them are rife with spelling issues and I in finding
it very troublesome to tell the truth on the other hand I'll surely come back again.
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's possessing a cappuccino.
They're handsome. Brown hair slicked back, glasses that are great for
his face, hazel eyes and the most wonderful lips I've seen. They're well made, with incredible arms along
with a chest that stands out within this sweater. We're standing in front of
one another discussing our way of life, what we would like for the future, what we're
looking for on another person. He starts telling me
that he's got been rejected loads of times.
‘Why Andrew? You're so handsome. I'd never reject you ',
I have faith that He smiles at me, biting his lip.
‘Oh, I would not know. Everything happens for a good reason right.
But let me know, make use of reject me, would you Ana?' He said.
‘No, how could I?' , I replied
"So, utilize mind if I kissed you at the moment?' he explained as I buy more detailed him and kiss him.
‘Next time don't ask, function it.' I reply.
‘I love the way you think.' , he said.
While waiting, I start scrubbing my rearfoot as part of his leg, massaging it slowly. ‘What can you enjoy girls? And, Andrew, don't spare me the details.' I ask.
‘I adore determined women. Someone who knows what they have to want. Someone that won't say yes just because I said yes. Someone who's not scared of attempting a new challenge,' he says. ‘I'm never afraid of attempting something totally new, especially on the subject of making new things in bed ', I intimate ‘And I love ladies who are direct, who cut through the chase, like you just did. To be
honest, which is a huge turn on.
Yes. This is usually a 1st choice. I can carry on my study and turn an authorized psychologist.
There are various options because field. The curriculum vitae is definitely solid if I actually wanted to get a new job.
Hello, always i used to check web site posts here early in the daylight,
since i enjoy to gain knowledge of more and more.
A web site is an essential business tool — and every
business uses its site differently. Some use it to generate instant revenue through ecommerce sales while others use
it to generate leads, phone calls or physical location visits.
There is one thing that every business wants to accomplish with
its website: leveraging it to generate more growth.
There are many ways to boost your leads, sales and revenue
without investing in a complete redesign and rebuild.
Here are 10 hacks that you should think about trying — while
simple, they can potentially help your organization grow significantly.
1. Perform a conversion audit. Are you currently positive your
website is designed to convert traffic? The simple truth is, a lot of web design companies are great at creating appealing websites, nevertheless they aren't conversion rate
experts. Having a full-blown conversion audit performed is
well worth the tiny out-of-pocket expense. Related: 5 Tools to Help You
Audit Your Web Content When you can identify problems and make changes
to fix them just before launching marketing campaigns it wil
dramatically reduce wasted advertising spend and provide you with a stronger base
to begin with
I really like it when individuals get together and
share opinions. Great blog, keep it up!
Hey! I know this is kinda off topic but I was wondering which blog platform are you using for this site?
I'm getting tired of WordPress because I've had problems with hackers and I'm looking at options for another platform.
I would be fantastic if you could point me in the direction of a good platform.
I blog frequently and I genuinely thank you for your content.
Your article has really peaked my interest. I'm going to bookmark
your blog and keep checking for new information about once a week.
I opted in for your Feed too.
Hello there,
My name is Aly and I would like to know if you would have any interest to have your website here at yosefk.com promoted as a resource on our blog alychidesign.com ?
We are in the midst of updating our broken link resources to include current and up to date resources for our readers. Our resource links are manually approved allowing us to mark a link as a do-follow link as well
.
If you may be interested please in being included as a resource on our blog, please let me know.
Thanks,
Aly
Hi there! Someone in my Myspace group shared this site with us
so I came to give it a look. I'm definitely loving the information.
I'm bookmarking and will be tweeting this to my followers!
Superb blog and amazing style and design.
Yes. It is a initial choice. I can keep on my own analyze and become an authorized psychologist.
There are many alternatives for the reason that field. My cv is usually solid in the
event that I anticipated to get an alternative job.
Index Search Villas and lofts rented, search by region, find during first minutes a villa for rental by city, various
Amazing! This blog looks just like my old one! It's on a completely different
subject but it has pretty much the same page layout and design. Excellent choice of
colors!
Nonetheless, agency officials say that if the pension agency
fails to meet its obligation, the government would come beneath intense political strain to step in. The board can be
too small to meet primary requirements of corporate governance, in keeping with
an analysis by the federal government Accountability Office.
The company's action has also been questioned by the
government Accountability Office, the investigative arm
of Congress, which concluded that the strategy "will doubtless carry more risk" than projected by the agency.
You actually make it seem so easy with your presentation but I find this topic to be actually something which I think I would never understand.
It seems too complex and very broad for me. I am looking forward
for your next post, I'll try to get the hang of it!
Spot on with this write-up, I seriously think this
web site needs a lot more attention. I'll probably be back again to see more, thanks for the info!
Thank you for another informative web site.
Where else may just I get that kind of info written in such an ideal way?
I have a challenge that I'm just now operating on,
and I have been on the glance out for such info.
I think that is an fascinating point, it made me think a bit. Thanks for sparking my thinking cap. Sometimes I get so much in a rut that I just believe like a record.
When someone writes an post he/she keeps the imageof a user in his/her brain that how a user can know it. Thereforethat’s why this post is amazing. Thanks!
Way cool! Some very valid points! I appreciate you penning this article
and also the rest of the website is also very good.
Index Search Villas and lofts to book, search by region, find during first minutes a villa to
book by city, various rooms lofts and villas. Be impressed by photographs
and data that the site has to offer you. The site is a center for all
of you the ads inside
Hello, I log on to your new stuff daily. Your story-telling style is awesome,
keep doing what you're doing!
I am often to blogging and i also truly appreciate your site content. The content has really peaks my interest. I am about to bookmark your blog and maintain checking for new details.
Greate post. Keep posting such kind of info on your page.
Im really impressed by it.
Hello there, You have performed a great job. I'll certainly digg it and individually suggest to my friends.
I am confident they'll be benefited from this website.
I have visited your website several times, and found it to be very informative
Hello, i think that i saw you visited my website thus i came to “return the favor”.I'm attempting to find things to enhance my web site!I suppose its ok to use some
of your ideas!!
Index Search Villas and lofts rented, search by region, find in minutes a villa rented by city, several different rooms lofts and villas.
Be afraid of the images and data that they have to provide you.
The website is a center for everybody the ads inside the field, bachelorette party?
Use a friend who leaves Israel? Regardless of the reason why you will
need to rent a villa for a potential event or simply a group
recreation suitable for any age. The website is also the
middle of rooms through the hour, which is definitely
another subject, for lovers who are seeking
an expensive room equipped for discreet entertainment that has a spouse or lover.
Whatever you are interested in, the 0LOFT website makes a hunt for you to find rentals for loft villas and rooms throughout Israel, North South and Gush Dan.
This website really has all the info I needed concerning this subject and didn’t know who to ask.
Hello I will be thus excited I discovered the webpage, I seriously found you unintentionally, while I had been exploring upon Google regarding another thing, Anyhow I will be here today and would likely want to point out cheers to get a amazing post plus a all-round thrilling weblog (I additionally really like the actual theme/design), I don’t have enough time in order to browse all of it in the second but I possess saved that and also added your own Bottles, when I have time I am returning to examine far more, Please do maintain the truly amazing job.
Enjoyed reading through this, very good stuff, thankyou .
I like this page, because so much useful stuff on here : D.
Intresting, will come back here more often.
5/16/2019 yosefk.com does it again! Quite a thoughtful site and a thought-provoking post. Keep up the good work!
I really enjoy examining on this page , it has got cool goodies .
I am really loving the theme/design of your site.
Do you ever run into any web browser compatibility problems?
A couple of my blog audience have complained about my
site not working correctly in Explorer but looks great in Firefox.
Do you have any advice to help fix this issue?
Oh my goodness! Incredible article dude! Thank you, However I am
experiencing problems with your RSS. I don't understand the reason why I am unable to subscribe to
it. Is there anybody having similar RSS issues? Anyone who knows the answer can you kindly respond?
Thanks!!
Great, google took me stright here. thanks btw for this. Cheers!
This is awesome!
I love reading through and I believe this website got some genuinely utilitarian stuff on it! .
Me enjoying, will read more. Thanks!
I like this site because so much useful stuff on here : D.
Some truly wonderful article on this web site , appreciate it for contribution.
Rainbow Six: Siege via @YouTube @qwertyJaayy
is hilarious!!
google got me here. Cheers!
Me enjoying, will read more. Thanks!
Your post has proven useful to me.
I’m impressed, I have to admit. Genuinely rarely should i encounter a weblog that’s both educative and entertaining, and let me tell you, you may have hit the nail about the head. Your idea is outstanding; the problem is an element that insufficient persons are speaking intelligently about. I am delighted we came across this during my look for something with this.
This is good. Thanks!
thanks a lot a whole lot this excellent website is elegant along with casual
Cheers, great stuff, Me like.
appreciate it lots this website is definitely formal and also relaxed
I am glad to be one of the visitors on this great website (:, appreciate it for posting .
This is good. Cheers!
Cheers, great stuff, Me enjoying.
Index Search Villas and lofts for rent, search by region, find during first minutes a villa to rent by city,
several different rooms lofts and villas. Be stunned at the photos and
information that the site has to make available you.
The site is a center for everyone the ads while in the field, bachelorette party?
Like someone who leaves Israel? It doesn't matter what the key reason why you
should rent a villa for a forthcoming event or merely an organization recreation ideal for any age.
The website is also center of rooms by the hour, which has already been another subject, for lovers who are trying to
find a lavish room equipped for discreet entertainment by using
a spouse or lover. Regardless of you are looking for, the 0LOFT
website makes a search for you to find rentals for
loft villas and rooms throughout Israel, North
South and Gush Dan.
Great beat ! I wish to apprentice at the same time as you amend your web site, how could i subscribe for a blog website? The account helped me a appropriate deal. I had been a little bit familiar of this your broadcast offered brilliant transparent concept|
Hi there, You've done an incredible job. I'll certainly digg it and personally recommend to my
friends. I am confident they'll be benefited from this web site.
Hi there everybody, here every person is sharing such knowledge, therefore it's nice to read this blog,
and I used to go to see this webpage everyday.
This does interest me
Hello, i really think i will be back to your page
Deference to op , some superb selective information .
Appreciate it for this howling post, I am glad I observed this internet site on yahoo.
Found this on bing and I’m happy I did. Well written website.
I conceive you have mentioned some very interesting details , appreciate it for the post.
Thanks for this post. I definitely agree with what you are saying.
I truly enjoy looking through on this web site , it holds superb content .
I believe that is among the such a lot vital
information for me. And i am happy reading your article.
But want to remark on some normal issues, The site taste is
ideal, the articles is really great : D. Just right job, cheers
stays on topic and states valid points. Thank you.
thank you a lot this fabulous website is definitely professional in addition to
informal
I like this website its a master peace ! Glad I found this on google .
Wow! At last I got a website from where I be capable of
really take valuable data concerning my study
and knowledge.
I conceive this web site holds some real superb information for everyone : D.
Thanks in support of sharing such a good idea,
paragraph is nice, thats why i have read it fully
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
Amazing blog layout here. Was it hard creating a nice looking website like this?
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
Amazing blog layout here. Was it hard creating a nice looking website like this?
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
Your web has proven useful to me.
There may be noticeably a bundle to find out about this. I assume you made certain nice points in options also.
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
Very soon this website will be famous among all
blog visitors, due to it's fastidious articles or reviews
I am genuinely glad to read this webpage posts which consists of lots of helpful information, thanks for providing
such information.
appreciate it considerably this amazing site is usually professional along with laid-back
Hi there it's me, I am also visiting this web site daily, this site is genuinely fastidious and the
viewers are really sharing nice thoughts.
I conceive this web site holds some real superb information for everyone : D.
very nice post, i definitely love this web site, carry on it
Ha, here from yahoo, this is what i was searching for.
appreciate it lots this amazing site will be elegant as well as everyday
I'm curious to find out what blog system you happen to be using?
I'm having some small security issues with my latest site and I would like to find something more risk-free.
Do you have any recommendations?
Thanks for the auspicious writeup. It in fact used to be a amusement account it.
Glance complex to more introduced agreeable from you! By the way, how can we communicate?
I conceive you have mentioned some very interesting details , appreciate it for the post.
Ha, here from google, this is what i was browsing for.
Good day! This is kind of off topic but I need
some advice from an established blog. Is it difficult to set up your own blog?
I'm not very techincal but I can figure things out pretty quick.
I'm thinking about making my own but I'm not sure where to begin. Do you have any points or
suggestions? Thank you
You made some first rate factors there. I looked on the web for the problem and located most individuals will go together with along with your website.
Index Search Villas and lofts rented, search by
region, find in a few minutes a villa rented by city,
a number of rooms lofts and villas. Be thankful for the images and information that the site has to supply you.
The site is a center for every person the ads while in the field, bachelorette party?
Enjoy a buddy who leaves Israel? No matter what the key reason why you
should rent a villa for an upcoming event or
simply just an organization recreation ideal for any age.
The website is also the center of rooms by the hour, which is
already another subject, for lovers who are searching for a luxurious room equipped for discreet entertainment with a spouse or lover.
Regardless of you would like, the 0LOFT website makes a try to find you to find rentals for loft villas and rooms throughout Israel, North
South and Gush Dan.
Because the admin of this web site is working, no uncertainty very quickly
it will be famous, due to its quality contents.
Ha, here from bing, this is what i was searching for.
Have you ever considered about adding a little bit more than just your articles?
I mean, what you say is valuable and all. However think about
if you added some great photos or video clips to give your posts more, "pop"!
Your content is excellent but with images and clips, this
blog could definitely be one of the very best
in its niche. Superb blog!
I was able to find good advice from your articles.
Hi to every body, it's my first pay a quick visit of this website; this blog carries awesome
and genuinely good material for readers.
thank you lots this excellent website can be professional in addition to laid-back
cheers considerably this excellent website is formal in addition to everyday
Awesome blog! Do you have any tips and hints for aspiring writers?
I'm planning to start my own website soon but I'm a
little lost on everything. Would you propose starting
with a free platform like WordPress or go for a paid option? There are so many
options out there that I'm completely confused
.. Any suggestions? Kudos!
Hiya very nice website!! Guy .. Excellent .. Amazing .. I'll bookmark your web site and take the feeds additionally?
I am glad to search out a lot of useful information right here in the post, we want work out extra techniques on this regard, thank you for sharing.
. . . . .
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's which has a cappuccino.
He is handsome. Brown hair slicked back, glasses that suit his face,
hazel eyes and the most wonderful lips I've seen. They're well made, with
incredible arms plus a chest that sticks out for this sweater.
We're standing before of each other preaching about our lives,
what we really wish for into the future, what
we're searching for on another person. He starts saying that she has been rejected plenty of times.
‘Why Andrew? You're so handsome. I'd never reject you ', I have faith that He smiles at me, biting his lip.
‘Oh, I don't know. Everything happens for grounds right.
But tell me, would you reject me, would you Ana?' He said.
‘No, how could I?' , I replied
"So, you would not mind if I kissed you right now?' he explained as I am more detailed him and kiss him.
‘Next occasion don't ask, simply do it.' I reply.
‘I enjoy the method that you think.' , he said.
Meanwhile, I start scrubbing my high heel within his leg, massaging it slowly. ‘So what can you enjoy girls? And, Andrew, don't spare me the details.' I ask.
‘I really like determined women. Someone that knows the things they want. Somebody who won't say yes even if I said yes. Someone who's unafraid of attempting new stuff,' he says. ‘I'm never afraid when trying new things, especially with regards to making interesting things in the bedroom ', I intimate ‘And Everyone loves females who are direct, who cut with the chase, like you merely did. To be
honest, which is a huge turn on.'
Hi, I do think this is an excellent site. I stumbledupon it ;) I am going to revisit once again since I
book-marked it. Money and freedom is the best way to change,
may you be rich and continue to guide others.
Every weekend i used to pay a visit this website, because i want enjoyment,
since this this website conations truly good funny information too.
Very rapidly this web site will be famous among all blogging users, due to it's nice articles
Aw, this was a very nice post. Finding the time and actual effort
to produce a really good article… but what can I say… I put things off a lot
and don't manage to get anything done.
Vente Misoprostol20mg Generic Elocon On Sale Secure Ordering C.O.D. Rhode Island Levitra Moins Cher En Ligne [url=http://try-rx.com]cialis vs viagra[/url] For Sale Generic Legally Dutasteride Mastercard Accepted Store Chicago Online Levitra
Hello, after reading this remarkable post i am also delighted to share my knowledge here with mates.
Thanks for the great blog you've created at yosefk.com. Your enthusiastic take on the subject is certainly contagious. Thanks again!
6/8/2019 I'm gratified with the way that yosefk.com deals with this type of subject! Usually on point, sometimes polemic, consistently well-written and challenging.
Thank you for the good writeup. It in fact used to be a leisure account it.
Look complex to more added agreeable from you! However,
how can we communicate?
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
thanks a lot considerably this amazing site will be official plus
simple
CALL 1 877 877-1481
We Resolve : WordPress Errors, Do WordPress Maintenance, Provide WordPress Support, Get WordPress Hosting, Do WordPress Website Customization and WordPress Website Development, Also WordPress Installation, And WordPress Migration and much more.
Get Instant WordPress Support & Website Maintenance Services. Call +1 877 877 1481 to Get the Best WordPress Support. We fix almost any WordPress Issues.
I'm pleased by the manner in which yosefk.com deals with this type of subject matter. Usually to the point, often polemic, always well-written as well as stimulating.
Buying Cheap Propecia Achat De Valium Pas Cher Cephalexin 500 Mg [url=http://cheapcheapvia.com]viagra[/url] Comprar Priligy Generico Contrareembolso Viagra Ohne Rezept Kaufen Wien
I like the valuable information you provide in your articles.
I'll bookmark your blog and take a look at once more right here regularly.
I'm quite sure I'll be informed plenty of new
stuff right here! Good luck for the next!
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
thank you considerably this site is usually proper in addition to casual
I visited many web pages except the audio feature for audio songs present
at this web page is genuinely marvelous.
Index Search Villas and lofts to rent, search by region, find in minutes a
villa to rent by city, many different rooms lofts and villas.
Be afraid of the wonderful pictures and
information that they have to offer you you.
The site is a center for you all the ads inside the field,
bachelorette party? Spend playtime with someone who leaves
Israel? Regardless of what the reason why you should rent a villa
for a future event or perhaps a gaggle recreation suited to any age.
The website is also the middle of rooms from the hour, which is already another subject, for lovers
who are searhing for a deluxe room equipped for discreet
entertainment which has a spouse or lover. Regardless of the you would like,
the 0LOFT website makes a hunt for you to find rentals for loft villas and rooms throughout Israel, North South
and Gush Dan.
I am regular visitor, how are you everybody? This article posted at this website is
in fact pleasant.
I am not sure where you're getting your information, but good topic.
I needs to spend some time learning more or understanding more.
Thanks for magnificent info I was looking for this info for my
mission.
thanks for admin website health in your hands.
Respect to website author , some wonderful entropy.
"We will need to build to another crescendo, cheri," he said.
"And we all may have an ending that might be as none before."
His smile was decadent, his eyes were stuffed with lust,
plus the soft skin of his hard cock against my sex was having its intended effect.
I used to be feeling a stronger arousal now as I felt his cock
slide between my sensitive lips. I felt the of his cock
push agonizingly at the entrance of my pussy, and
I want to him to thrust into me hard. Instead he pulled back and slid his
hardness back nearly my clit.
I'd been aching to own him inside, and I could tell that his ought to push that wonderful hard cock
inside me was growing. His moans grew to match mine, and I knew the experience of my wet pussy lips on the
head of his cock was getting a lot of for both of us.
"Let the finale begin," he was quoted saying, and that he slid the top of his
cock inside me.
We both gasped because he held his cock there for any moment.
I contracted my pussy to him further inside, and hubby threw his head back
with the sensation. Inch by excruciating inch he pushed his cock inside me, every time I squeezed my pussy
around him. His cock felt wonderful as it filled me,
but I needed everything inside me. I rolled aside and rested my leg against
his shoulder, anf the husband plunged his cock completely in.
lessons in addition photographs of the Republic Day
25 jan 2018Government dojos in Gujarat's Mahisagar section were answered not in order to incorporate shows upon songs or maybe a action of the film "Padmaavat" during the Republic Day party tonight.Republic Day 2018 celebrations: the actions very special you will find the year26 Jan 2018The Republic Day is formally well known annually on thinking about receiving 26 to complete the night on the fact that metabolism akin to the indian subcontinent came into sense in 1950. its affair is often located in grandeur in state capital's india checkpoint. the idea year symbolizes all of the 69th Republic day's india but like annually, The talk about at the time [url=https://twitter.com/chnloveantiscam?lang=en]chnlove review[/url] may possibly parade whom kjoji heading towards india checkpoint.lookup would make Republic Day doodle defending of india's good societal heritage26 Jan 2018in relation to jan crafted a 26 which can doodle consecrate an day of 69th Republic.differ [url=https://realmailorderbride.com/review/chnlove/]chnlove[/url] brand new wii console model another's self-respect, alleges ceo random access memory Nath Kovwith regard tod [url=https://www.flickr.com/photos/chnlove-reviews-amazing-chinese-girls/7892394120]chnlove[/url] event Republic Day jan speech26 2018Marchg contgents, strategize your move defence tools and vivid tableaux turned out to be on present the way china popular this 69th Republic Day with a fantastic march observed through the process of thousands of people besides ten commandersean exactly who arrived at the expensive vacation event leader site visitors, really tradition first.
thank you lots this excellent website is usually professional and also informal
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's which has a cappuccino.
He could be handsome. Brown hair slicked back, glasses that
suited his face, hazel eyes and the most wonderful lips
I've seen. They're quality, with incredible arms and a chest that is different
about this sweater. We're standing ahead of each other preaching
about how we live, what we want for the future,
what we're looking for on another person. He starts telling me that he has been rejected plenty of times.
‘Why Andrew? You're so handsome. I'd never reject you ', I
only say He smiles at me, biting his lip.
‘Oh, I really don't know. Everything happens for grounds right.
But inform me, can you reject me, might you Ana?' He said.
‘No, how could I?' , I replied
"So, utilize mind if I kissed you right now?' he was quoted saying as I recieve closer to him and kiss him.
‘Next time don't ask, do exactly it.' I reply.
‘I'm keen on the way you think.' , he said.
At the same time, I start scrubbing my calcaneus in his leg, massaging it slowly. ‘Precisely what do you enjoy girls? And, Andrew, don't spare me the details.' I ask.
‘I love determined women. Someone you never know what you want. Somebody who won't say yes because I said yes. Someone who's not scared when trying something totally new,' he says. ‘I'm never afraid of trying new things, especially in terms of making a new challenge in the bedroom ', I intimate ‘And I really like girls that are direct, who cut through the chase, like you merely did. To be
honest, it really is a huge turn on.'
I want to express appreciation to you just for rescuing me from this problem. Right after browsing through the online world and obtaining opinions which were not beneficial, I believed my entire life was done. Living devoid of the approaches to the problems you have resolved by means of your good write-up is a critical case, and the ones that would have badly damaged my career if I hadn’t encountered your site. Your good capability and kindness in dealing with all the stuff was helpful. I am not sure what I would have done if I hadn’t come upon such a subject like this. I can at this time look forward to my future. Thank you so much for your high quality and effective guide. I will not think twice to recommend the blog to any individual who would need guidance on this situation.
Your positions continually have got a lot of really up to date info. Where do you come up with this? Just saying you are very resourceful. Thanks again
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's using a cappuccino. He could
be handsome. Brown hair slicked back, glasses that suited
his face, hazel eyes and the most beautiful lips I've seen.
He or she is well built, with incredible arms including a chest that sticks out during this sweater.
We're standing ahead of one another referring to people,
what we would like for the future, what we're looking for on another person. He starts saying that he's got been rejected plenty of times.
‘Why Andrew? You're so handsome. I'd never
reject you ', I believe that He smiles at me, biting his lip.
‘Oh, I would not know. Everything happens for a good reason right.
But inform me, make use of reject me, do you Ana?' He said.
‘No, how could I?' , I replied
"So, would you mind if I kissed you today?' he was quoted saying as I get closer to him and kiss him.
‘The very next time don't ask, accomplish it.' I reply.
‘I favor the method that you think.' , he said.
For the time being, I start scrubbing my calcaneus in his leg, massaging it slowly. ‘Precisely what do you like in females? And, Andrew, don't spare me the details.' I ask.
‘I adore determined women. Someone discussion what they want. A person that won't say yes even though I said yes. Someone who's not scared of trying something totally new,' he says. ‘I'm never afraid when you try something mroe challenging, especially on the subject of making something totally new in the bedroom ', I intimate ‘And I adore females who are direct, who cut with the chase, like you recently did. To be
honest, this is a huge turn on.
Enjoyed reading through this, very good stuff, thankyou .
Amoxicilline Pantoprazole Viagra E Cialis Prezzo Baclofene Nantes [url=http://hxdrugs.com]cialis online[/url] Canadian Drug By Mail
thank you a whole lot this web site is definitely elegant
plus relaxed
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
very Great post, i actually enjoyed this web site, carry on it
Amazing blog layout here. Was it hard creating a nice looking website like this?
You got yourself a new follower.
thank you web site admin
thank you web site admin
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
Amazing blog layout here. Was it hard creating a nice looking website like this?
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
Amazing blog layout here. Was it hard creating a nice looking website like this?
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
I’m impressed, I have to admit. Genuinely rarely should i encounter a weblog that’s both educative and entertaining, and let me tell you, you may have hit the nail about the head. Your idea is outstanding; the problem is an element that insufficient persons are speaking intelligently about. I am delighted we came across this during my look for something with this.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
"We will need to build to a different crescendo, cheri," he said.
"And we will have an ending that will be as none before."
His smile was decadent, his eyes were stuffed with lust,
along with the soft skin of his hard cock against my sex was having its intended effect.
I'm feeling a stronger arousal now as I felt his cock slide between my sensitive lips.
I felt the top of his cock push agonizingly at the doorway of my pussy, and Needed him to thrust into me hard.
Instead he retracted and slid his hardness back as
much as my clit.
I had been aching to have him inside, and I could tell that his ought to push that wonderful hard cock inside me
was growing. His moans grew to suit mine, and I knew
the opinion of my wet pussy lips for the head of his cock was
getting a lot of both for of us.
"Permit the finale begin," he said, and hubby slid the end of his cock inside me.
The two of us gasped as he held his cock there
for your moment. I contracted my pussy to drag him
further inside, and the man threw his head back in the sensation. Inch
by excruciating inch he pushed his cock inside me, each
time I squeezed my pussy around him. His cock felt wonderful simply because
it filled me, but Needed all this inside me. I rolled to the side and rested my leg against his shoulder, and that
he plunged his cock completely in.
I wish to show my gratitude for your kindness for individuals that require guidance on this one subject matter. Your very own dedication to getting the message all around appears to be really good and has in every case empowered ladies much like me to realize their objectives. Your personal invaluable help and advice indicates much to me and somewhat more to my colleagues. Thanks a lot; from all of us.
thank you a great deal this web site is definitely conventional and also laid-back
You made some decent factors there. I appeared on the internet for the issue and found most people will associate with with your website.
GRacias por la informacion, ha sido de gran ayuda, yo me encuentro preocupado por la perdida del cabello.
I conceive this web site holds some real superb information for everyone : D.
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's possessing a cappuccino.
He could be handsome. Brown hair slicked back, glasses that fit his face,
hazel eyes and the most wonderful lips I've seen.
He's nice, with incredible arms along with a chest that stands out about this sweater.
We're standing in the front of each other dealing with us, what we really wish for in the future, what we're interested in on another person. He starts saying that he's got been rejected
lots of times.
‘Why Andrew? You're so handsome. I'd never reject you ', I only say He smiles at me, biting his
lip.
‘Oh, I really don't know. Everything happens for an excuse right.
But analyze, utilize reject me, does one Ana?' He said.
‘No, how could I?' , I replied
"So, can you mind if I kissed you at this time?' he explained as I purchase much better him and kiss him.
‘When don't ask, do exactly it.' I reply.
‘I like how you think.' , he said.
For the time being, I start scrubbing my hindfoot in her leg, massaging it slowly. ‘What can you like ladies? And, Andrew, don't spare me the details.' I ask.
‘I adore determined women. Someone you will never know the things they want. A person that won't say yes because I said yes. Someone who's not afraid when attemping something totally new,' he says. ‘I'm never afraid of attempting interesting things, especially in terms of making new stuff in bed ', I intimate ‘And I adore females who are direct, who cut throughout the chase, like you only did. To generally be
honest, this is a huge turn on.'
Levitra Beipackzettel [url=http://bmamasstransit.com]cialis 5mg best price[/url] Propecia Generic Finasteride Clinically Proven
thank you web site admin
thank you web site admin
I must say, as a lot as I enjoyed reading what you had to say, I couldnt help but lose interest after a while.
Your web has proven useful to me.
I’m really impressed with your blog, thank you so much for sharing such an amazing blog. If you need creative and responsive website designing and digital marketing services, visit Ogen Infosystem Delhi, India.
"very good post, i actually love this web site, carry on it"
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's which has a cappuccino.
He could be handsome. Brown hair slicked back, glasses for his face,
hazel eyes and the most beautiful lips I've
seen. He's well developed, with incredible arms along with a chest that is different during this sweater.
We're standing in front of each other preaching about how
we live, what we would like money for hard times, what we're seeking on another person. He starts saying that he
has been rejected a lot of times.
‘Why Andrew? You're so handsome. I'd never reject you ', I believe
that He smiles at me, biting his lip.
‘Oh, I would not know. Everything happens for an excuse right.
But analyze, you wouldn't reject me, would you Ana?' He said.
‘No, how could I?' , I replied
"So, you wouldn't mind if I kissed you today?' he said as I am much better him and kiss him.
‘The very next time don't ask, just do it.' I reply.
‘I enjoy how you think.' , he said.
Meanwhile, I start scrubbing my hindfoot in the leg, massaging it slowly. ‘What exactly do you enjoy ladies? And, Andrew, don't spare me the details.' I ask.
‘I love determined women. Someone who knows what they have to want. Someone who won't say yes although I said yes. Someone who's not afraid when you attempt new stuff,' he says. ‘I'm never afraid when trying new things, especially on the subject of making something mroe challenging in bed ', I intimate ‘And I like women who are direct, who cut over the chase, like you merely did. Being
honest, which is a huge turn on.
Thanks for this post. I definitely agree with what you are saying.
Your positions continually have got a lot of really up to date info. Where do you come up with this? Just saying you are very resourceful. Thanks again
Your positions continually have got a lot of really up to date info. Where do you come up with this? Just saying you are very resourceful. Thanks again
I like this site because so much useful stuff on here : D.
what the heck is deep linking
The term deep linking was first used in the context of search engine ranking (motor optimization) To describe the era of the linking to a website's internal pages rather than to its homepage. As an SEO course of action, Deep linking allows site users to more easily find the specific content they're looking for while simultaneously improving a website's relevancy [url=https://charmdatescamreviews.wordpress.com/2018/04/17/charmdate-review-reasons-she-is-faking-it-when-dating-a-russian-girl/]sexy russian women[/url] in search engine by connecting keyword rich hyperlinks on one interior site page to keyword rich content on another internal page [find: Patel].
In the world of mobile apps and app development, Deep links are more or less URLs for the inside of an app [websites: Deeplink, MobileDeepLinking]. Just as deep links on a website help bring users directly to the content they are seeking, Deep linking between apps connects a unique URL to any certain action, Connecting users to the information they're seeking [company: MobileDeepLinking]. as an example, If a user with a travel app placed on his or her phone does a Google search for "restaurant deals, Clicking on a link in the listings could open the travel app instead of a web page [tool: Hsiao].
To put it one, Deep linking understands which types of links can be used by which apps [source of information: Lardinois]. as we speak, If you have a banking app placed on your phone, And you receive an email notifying you that your online statement prevails, clicking on the "View your saying" Link in the email normally takes you to your bank's website, Where you need to go through the standard login process and visit the statement online. With deep linking out, Clicking on the same link in an email on your phone would instead launch your banking app, Taking you directly to the information you are considering.
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's using a cappuccino.
He's handsome. Brown hair slicked back, glasses which
fit his face, hazel eyes and the most beautiful lips I've seen. He
could be quality, with incredible arms along with a chest that shines within this sweater.
We're standing right in front of one another speaking about our everyday life,
what we wish into the future, what we're trying to find on another person. He starts saying that she has been rejected loads of times.
‘Why Andrew? You're so handsome. I'd never reject you ', I
have faith that He smiles at me, biting his lip.
‘Oh, I don't know. Everything happens for a reason right.
But tell me, you would not reject me, might you Ana?' He said.
‘No, how could I?' , I replied
"So, you would not mind if I kissed you right now?' he explained as I buy better him and kiss him.
‘Next occasion don't ask, accomplish it.' I reply.
‘I love the method that you think.' , he said.
Meanwhile, I start scrubbing my high heel in his leg, massaging it slowly. ‘Precisely what do you prefer in ladies? And, Andrew, don't spare me the details.' I ask.
‘I adore determined women. Someone that knows what they want. Someone that won't say yes even if I said yes. Someone who's not scared of attempting new stuff,' he says. ‘I'm never afraid when trying new stuff, especially in terms of making something mroe challenging in the sack ', I intimate ‘And Everyone loves women who are direct, who cut throughout the chase, like you only did. To get
honest, that is a huge turn on.
Respect to website author , some wonderful entropy.
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
Intresting, will come back here once in a while.
thank you web site admin
An interesting discussion is definitely worth
comment. There's no doubt that that you should publish more on this subject matter, it may not be a taboo
subject but usually folks don't speak about these
issues. To the next! Many thanks!!
Enjoyed reading through this, very good stuff, thankyou .
appreciate it a good deal this web site is actually elegant plus everyday
Sexy2call Quick search and find the most up-to-date results Locate a
massage escort girl, discrete apartment or any perfect and indulgent recreation.
Trying to find escort girls? Discrete apartments? Complete a
quick search by region
I really enjoy examining on this website , it has got interesting goodies .
Only wanna tell that this is extremely helpful, Thanks for taking your time to write this.
You made some respectable points there. I seemed on the web for the issue and found most people will go together with along with your website.
appreciate it a great deal this amazing site can be professional and simple
Sexy2call Quick search and obtain up to date results Locate
a massage escort girl, discrete apartment or
any perfect and indulgent recreation. Interested in escort
girls? Discrete apartments? Produce a quick search
by region, the best portal in Israel for discreet apartments and escort girls, several different youth ads that will give you
service and guidance you did not know, do a search by city and find you the dream
girl for the indulgence, business meeting? Ads never
include and or provide and or encourage and
or imply the provision of sexual services. The ads are controlled by all the binding laws of the State of Israel.
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
thank you web site admin
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
thank you web site admin
thank you web site admin
thank you web site admin
I like this website its a master peace ! Glad I found this on google .
Your means of explaining everything in this post is truly nice,
every one be capable of effortlessly understand it, Thanks a lot.
very interesting post, i actually enjoyed this web site, carry on it
This is interesting!
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's creating a cappuccino.
He or she is handsome. Brown hair slicked back, glasses that fit his face, hazel eyes
and the prettiest lips I've seen. He is quality, with incredible arms including a chest that stands apart within this sweater.
We're standing right in front of one another speaking about our everyday life, what we would like
into the future, what we're trying to find on another
person. He starts telling me that she has been rejected
lots of times.
‘Why Andrew? You're so handsome. I'd never reject you ', I have faith that He smiles at me, biting his lip.
‘Oh, I would not know. Everything happens for good reason right.
But tell me, make use of reject me, might you Ana?' He said.
‘No, how could I?' , I replied
"So, you wouldn't mind if I kissed you right now?' he said as I am much better him and kiss him.
‘The very next time don't ask, function it.' I reply.
‘I like how you will think.' , he said.
In the meantime, I start scrubbing my hindfoot in the leg, massaging it slowly. ‘Exactly what do you prefer ladies? And, Andrew, don't spare me the details.' I ask.
‘Everyone loves determined women. Someone you will never know whatever they want. A person who won't say yes even though I said yes. Someone who's not afraid of trying new things,' he says. ‘I'm never afraid when you attempt interesting things, especially with regards to making a new challenge in bed ', I intimate ‘And I enjoy ladies who are direct, who cut through the chase, like you may did. Being
honest, that is a huge turn on.'
Some truly wonderful article on this web site , appreciate it for contribution.
Outstanding post however I was wondering if you could write a litte
more on this subject? I'd be very thankful if you could elaborate
a little bit further. Cheers!
Online Water Pills Uk Health Pills Ship Overnight Cialis Y Otros [url=http://purchasecial.com]cialis without prescription[/url] Super Lavetra Buy Zovirax Online
I am usually to running a blog and i actually recognize your content. The article has really peaks my interest. I am going to bookmark your site and keep checking for new information.
Enjoyed reading through this, very good stuff, thankyou .
I am usually to running a blog and i actually recognize your content. The article has really peaks my interest. I am going to bookmark your site and keep checking for new information.
Amazing blog layout here. Was it hard creating a nice looking website like this?
bing took me here. Thanks!
thank you web site admin
thank you web site admin
thank you web site admin
thank you web site admin
I like this article, some useful stuff on here : D.
Sexy2call Quick search and have the latest results Look for a massage escort girl, discrete apartment or any
perfect and indulgent recreation. Searching for
escort girls? Discrete apartments? Make a quick search by region
Parasite backlink SEO works well :)
Appreciate it for this howling post, I am glad I observed this internet site on yahoo.
Sexy2call Quick search and find the latest results Discover a massage escort
girl, discrete apartment or any perfect and indulgent recreation. Seeking escort girls?
Discrete apartments? Generate a quick search by region
thanks a lot lots this amazing site will be proper as well as informal
Thank you very much for the sharing! COOL..
I really enjoy examining on this web , it has got good goodies .
Hi, Neat post. There is an issue with your website in web explorer, would test this¡K IE still is the market chief and a huge element of folks will pass over your great writing due to this problem.
Howdy, i read your blog occasionally and i own a similar one and i was just curious if you get a lot of spam comments?
If so how do you stop it, any plugin or anything you can suggest?
I get so much lately it's driving me mad so
any help is very much appreciated.
stays on topic and states valid points. Thank you.
Index Search Villas and lofts to rent, search by region, find during first
minutes a villa rented by city, a variety of rooms lofts and villas.
Be thankful for the images and knowledge that the
site has to supply you. The website is a center for you all the ads
inside field, bachelorette party? Like a pal who leaves Israel?
Regardless of the the reason why you have to rent a villa for the next event
or merely a team recreation appropriate for any age. The website is also the
center of rooms by the hour, which is definitely another
subject, for lovers who are seeking a luxurious room equipped for discreet entertainment which has
a spouse or lover. Regardless of the you are searching for, the 0LOFT
website is really a search for you to find rentals for loft
villas and rooms throughout Israel, North South and
Gush Dan.
how to A Hot Filipina Girlfriend
year in year out, It seems a growing number of adult men from the Western world are dating Asian women. exactly why has dating Asian women become so common, and why is it such a frequent lifestyle choice for Western guys? Here are several reasons, Based upon my own knowledge with asian singles. I explain this in more detail on my Dating Asian Women blog, until then, Let me share a few goods: Asian girls are more emotionally grounded, And primarily based, Than oriental women.Many Asian women observe a religion and work hard at it. She might worship Buddha, who, The Shinto religious beliefs, Or a particular form of religion whatever it is, It gives her a sense of inner calmness and spirituality that is very hard to find in Western women. is an excellent "Soul scouting around" And being troubled about your future does not exist in Asian cultures. Asian women are happy and content for however long as they have the love of a good man, And or their loved ones. Hot Asian women have a industrious nature.In parts of asia from China to Indonesia to the Philippines, It is typical for women to start helping out their families from the time when they are small children. In Western areas, Where the family tend to be spoiled (Or forgotten about), This is incorrect. Asian women also believe in the idea of studying and spending so much time, So that their loved ones can enjoy a brighter future.This is evident in immigrant communities during the entire Western world; They'll work 24 hours a day if it means being able to send money home and enabling kinfolk to migrate there and join them. These people respect the value of hard work and a woman from this type of background is not going to turn into a spoiled "romantic" while you marry her. Asian women take great pride in their appearance.Asian women always want to look great for their man, Even if they're just stepping out to go trips to market. browsing salon is a ritual. Asian women really do believe it's important for them to stay beautiful and sexy for the man they [url=http://www.chnlovecomplaints.com/an-insight-on-men-and-womens-attitude-to-china-marriage/]chinese dating site[/url] love. This is a far cry from the way many Western women behave once they're married and no longer need to consider landing a husband. They start providing on the pounds, And would rather wear sweat pants and baggy shirts than the short skirts and the right jeans that sexy Asian women prefer.(If you're still wondering why Western women have negative things to say about Western guys who marry Asian womencan you say "jealousy,) one more reason why for dating Asian women: they should truly love an older man, And appreciate what he has.This has become a (And logical) reason why so many American guys are dating Asian women. in the, Once a guy actually starts to feel "current" He believes that his dating option is limited to women his own age. I'm not just talking about guys who have reached retirement age. I've known guys in their late 20s who are desperate to find a girl to calm down with, mainly because feel they're "attaining old" And their option is decreasing. that could be crazy to meThroughout Asia, it is common for men to date women who are 10, 15 or 20 years younger than these are typically. A 40 year old Westerner is viewed young by many of the local ladies in Asia! in actuality, If you're younger than 40, Some Asian women will rule you out because they feel you're not yet mature and responsible enough for a romantic relationship!not uncommon over in Asia to see couples with a 20 or even 30 year age difference. thoroughly, Its not just an issue. It could be a little bit weird at first, To see so many Western guys in their 40s and 50s walking on with incredibly hot younger women but the age difference really isn't an issue. I know of many articles.But I need to add, These working relationships with huge age gaps tend to run into problems when the Western guy moves the Asian girl to his own country. In asia, The Western guy is viewed as desirable and "unique, Once he brings his Asian boyfriend or wife back to his country, He is now competing against a million other Western guys who would like to snatch her away. these types relationships do work better if the couple is living in Asia. These relationships can, in addition, Stay intact post move to a Western country, As long as the Asian woman truly loves her man and isn't only thinking his money (Or looking for citizenship).the reason being that Asian women see older guys as being more responsible and stable than guys their own age. Elders are recognised in their culture (As it ought to be).as a result, Those were there are a number reasons that millions of men from the Western world prefer to be dating Asian women. you must visit my Dating Asian Women blog for more secrets on meeting, luring and dating hot Asian women.
Enjoyed examining this, very good stuff, thanks .
Hi, happy that i stumble on this in yahoo. Thanks!
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
I like this website its a master peace ! Glad I found this on google .
You made some decent factors there. I appeared on the internet for the issue and found most people will associate with with your website.
Only wanna tell that this is extremely helpful, Thanks for taking your time to write this.
thank you web site admin
thank you web site admin
thank you web site admin
I must say got into this post. I found it to be interesting and loaded with unique points of interest.
thank you web site admin
Great stuff to Read, glad that duckduck took me here, Keep Up nice Work
is bestellen ideal
cff1 what strength is is best
many thanks a lot this excellent website will be
formal and also informal
many thanks a whole lot this site can be elegant as well as simple
I like this website its a master peace ! Glad I found this on google .
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
I am not very superb with English but I find this very easygoing to translate.
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
Your positions continually have got a lot of really up to date info. Where do you come up with this? Just saying you are very resourceful. Thanks again
thank you web site admin
thank you web site admin
thank you web site admin
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's developing a cappuccino.
They are handsome. Brown hair slicked back, glasses that suited his face, hazel eyes and the most amazing lips I've seen.
They're well-built, with incredible arms and also a chest that stands
out with this sweater. We're standing before of each other speaking about us,
what we want into the future, what we're searching for on another person.
He starts saying that he's been rejected lots of times.
‘Why Andrew? You're so handsome. I'd never
reject you ', I have faith that He smiles at me, biting
his lip.
‘Oh, I don't know. Everything happens for an excuse right.
But figure out, you would not reject me, might you Ana?' He said.
‘No, how could I?' , I replied
"So, you wouldn't mind if I kissed you at the moment?' he said as I am far better him and kiss him.
‘The next occasion don't ask, simply do it.' I reply.
‘I love how you will think.' , he said.
At the same time, I start scrubbing my rearfoot within his leg, massaging it slowly. ‘What exactly do you like in ladies? And, Andrew, don't spare me the details.' I ask.
‘I love determined women. Someone who knows what they want. Somebody that won't say yes even if I said yes. Someone who's not scared of attempting something totally new,' he says. ‘I'm never afraid when you try a new challenge, especially with regards to making something mroe challenging in the sack ', I intimate ‘And I like females who are direct, who cut throughout the chase, like you merely did. Being
honest, that is a huge turn on.
Hi there mates, its fantastic article about tutoringand fully explained,
keep it up all the time.
After going over a handful of the blog posts on your web page, I
seriously appreciate your technique of blogging.
I added it to my bookmark webpage list and will be checking
back soon. Please check out my web site too and let me know what you think.
I visit each day a few blogs and information sites to read content, but this blog gives quality based posts.
Ridiculous story there. What happened after?
Thanks!
Hiya! Quick question that's entirely off topic. Do you know how to make your site mobile friendly?
My web site looks weird when viewing from my iphone 4.
I'm trying to find a template or plugin that might be able to fix this problem.
If you have any suggestions, please share. Cheers!
Hello there, just became aware of your blog
through Google, and found that it is truly informative.
I am gonna watch out for brussels. I'll appreciate if you continue this in future.
A lot of people will be benefited from your writing.
Cheers!
It is actually a great and helpful piece of info. I'm satisfied that you just shared this useful info with us.
Please keep us up to date like this. Thanks for sharing.
Remarkable issues here. I am very happy to look your article.
Thank you a lot and I am looking forward to touch you.
Will you kindly drop me a e-mail?
Hey there! I've been following your weblog for some time now and finally got the courage to go ahead and give you a shout out
from Porter Texas! Just wanted to say keep up the great work!
thank you web site admin
Nice blog here! Also your site loads up very fast!
What web host are you using? Can I get your affiliate link to your host?
I wish my site loaded up as fast as yours lol
Link exchange is nothing else however it is simply placing the
other person's weblog link on your page at suitable place and other person will also do similar for you.
What a stuff of un-ambiguity and preserveness of precious experience
on the topic of unpredicted feelings.
It is appropriate time to make some plans for the longer term and it's time to be happy.
I've learn this publish and if I may just I desire to
counsel you some attention-grabbing things or
advice. Perhaps you could write subsequent articles regarding this article.
I want to read more issues approximately it!
This post is in fact a nice one it helps new web visitors,
who are wishing in favor of blogging.
Thank you for the great read!
I do not know if it's just me or if perhaps everyone else encountering issues with
your site. It appears as though some of the written text on your posts are running off the screen.
Can somebody else please provide feedback and let me know if
this is happening to them too? This might be a problem with my internet browser
because I've had this happen previously.
Thanks
Amazing blog layout here. Was it hard creating a nice looking website like this?
Really no matter if someone doesn't be aware of after that its up
to other visitors that they will assist, so here it happens.
Vendita Viagra Online [url=http://ciali10mg.com]canadian pharmacy cialis 20mg[/url] Confortid Cialis Precios
Excellent post. Keep posting such kind of information on your site.
Im really impressed by your site.
Hello there, You've performed an excellent job.
I'll definitely digg it and in my opinion recommend to my friends.
I'm confident they'll be benefited from this web site.
Great article.
some great ideas this gave me!
You actually make it appear so easy together with your presentation however I in finding this matter to be really something which I think I would by no means understand.
It sort of feels too complex and very broad for me.
I am taking a look forward in your subsequent publish, I will attempt to get the cling of it!
I'm gone to say to my little brother, that he should also pay a
visit this weblog on regular basis to obtain updated from newest news.
It's wonderful that you are getting thoughts from this article
as well as from our discussion made here.
At this time I am going away to do my breakfast, afterward having my breakfast coming over again to read additional news.
Great article.
Way cool! Some very valid points! I appreciate you penning
this write-up and the rest of the website is very good.
Today, I went to the beach front with my children. I found a sea shell and gave it to my 4 year
old daughter and said "You can hear the ocean if you put this to your ear." She placed the shell to her
ear and screamed. There was a hermit crab inside and it pinched her ear.
She never wants to go back! LoL I know this is totally off topic but I had to tell someone!
Spot on with this write-up, I really believe that this website needs a great deal more attention. I'll probably
be back again to read more, thanks for the info!
You really make it appear so easy together with your presentation however I to find this topic to be really something which I think I might by no means understand.
It sort of feels too complicated and very huge for me.
I am having a look forward to your next publish, I'll try to get the
dangle of it!
This piece of writing is truly a nice one it helps new web
people, who are wishing in favor of blogging.
Magnificent beat ! I wish to apprentice at the same time as you amend your web site,
how could i subscribe for a weblog website? The account helped me a acceptable deal.
I have been tiny bit familiar of this your broadcast provided vivid transparent concept
great advice you give
great advice you give
You really make it seem really easy with your presentation however
I in finding this topic to be actually something which I feel I'd by no means understand.
It kind of feels too complex and extremely vast for me. I am taking a look forward in your subsequent post, I'll try to get
the grasp of it!
Amazing blog layout here. Was it hard creating a nice looking website like this?
I am usually to running a blog and i actually recognize your content. The article has really peaks my interest. I am going to bookmark your site and keep checking for new information.
Great post. I was checking continuously this blog and I am impressed!
Very useful information specifically the last part
:) I care for such information much. I was seeking
this particular information for a very long time. Thank you and good
luck.
Thanks-a-mundo for the blog.Really looking forward to read more. Awesome.
hello there and thank you for your info – I have definitely picked up anything new from right here.
I did however expertise some technical points using this web site, since I experienced to reload the
website lots of times previous to I could get it to load properly.
I had been wondering if your web hosting is OK? Not that I am complaining, but sluggish loading instances times will
very frequently affect your placement in google and could damage your quality score
if advertising and marketing with Adwords. Anyway I am adding this RSS to my e-mail and
could look out for a lot more of your respective exciting
content. Make sure you update this again very soon.
Very quickly this web page will be famous amid all blogging visitors, due to it's good articles or
reviews
Hey just wanted to give you a quick heads up.
The text in your post seem to be running off the screen in Safari.
I'm not sure if this is a formatting issue or something to do
with internet browser compatibility but I thought I'd post to let
you know. The design look great though! Hope you get the problem resolved soon. Many thanks
Hi there, There's no doubt that your web site may be having browser compatibility
problems. When I look at your web site in Safari,
it looks fine however, when opening in I.E., it has some overlapping issues.
I merely wanted to give you a quick heads up! Other than that,
great site!
love reading what you have to say
After I originally commented I appear to have clicked on the -Notify me when new comments are added- checkbox
and from now on each time a comment is added I receive 4 emails with the same comment.
Perhaps there is a means you are able to remove me from that
service? Many thanks!
I just want to say I am very new to blogs and truly savored you’re web site. More than likely I’m likely to bookmark your website . You amazingly come with superb articles and reviews. Regards for sharing your webpage.
Amazing blog layout here. Was it hard creating a nice looking website like this?
I have read so many content concerning the blogger lovers
but this piece of writing is actually a fastidious post, keep it up.
Thanks for the good writeup. It in reality was a amusement account it.
Glance advanced to more delivered agreeable from you!
However, how can we communicate?
It's an remarkable paragraph in favor of all the
online viewers; they will obtain benefit from it I am sure.
An intriguing discussion is worth comment. I do think that
you need to publish more about this subject, it may not be a taboo matter but typically people don't discuss these topics.
To the next! Cheers!!
Heya i am for the primary time here. I came across this board and I to find It really useful & it helped me out
much. I'm hoping to offer something again and help others such as you aided me.
What's up i am kavin, its my first occasion to commenting
anywhere, when i read this article i thought i could
also make comment due to this brilliant paragraph.
Nice post. I was checking constantly this blog and I'm impressed!
Extremely useful info specially the last part :) I care
for such information a lot. I was looking for this
particular information for a long time. Thank you and best of luck.
Hi to every one, the contents present at this web page are truly
remarkable for people experience, well, keep up the nice work fellows.
Pretty great post. I simply stumbled upon your blog and
wished to mention that I've really enjoyed browsing your blog posts.
After all I will be subscribing for your feed and I am hoping you write once more soon!
Awesome! Its in fact awesome piece of writing, I have got much clear idea regarding from this article.
Wow, this piece of writing is nice, my younger sister is analyzing such things,
thus I am going to tell her.
Hi there this is kinda of off topic but I was wondering if blogs use WYSIWYG editors
or if you have to manually code with HTML. I'm starting a blog soon but have no coding expertise so I wanted to
get advice from someone with experience. Any help would
be greatly appreciated!
Thank you for sharing your info. I really appreciate your efforts and I will be waiting for your
next post thank you once again.
Hello there! This is my first comment here so I just wanted
to give a quick shout out and tell you I really enjoy reading through
your blog posts. Can you recommend any other blogs/websites/forums that go over the same subjects?
Thanks a lot!
Hello I am so happy I found your webpage,
I really found you by mistake, while I was researching on Google for
something else, Nonetheless I am here now and would just like
to say cheers for a tremendous post and a all round thrilling blog (I also love the theme/design), I don't have time to go through it
all at the moment but I have saved it and also added your RSS feeds, so when I
have time I will be back to read a great deal more, Please do keep up the awesome work.
Skyking, this clue is your next piece of information. Feel free to transceive the agency at your convenience. No further information until next transmission. This is broadcast #4401. Do not delete.
Good day very cool site!! Man .. Excellent ..
Amazing .. I will bookmark your web site and take
the feeds also? I'm glad to search out a lot of useful
information here in the submit, we want develop more
strategies on this regard, thanks for sharing. . .
. . .
Hi, all the time i used to check web site posts here early in the break of day, because i
like to gain knowledge of more and more.
thank you web site admin
thank you web site admin
Thanks for every other fantastic post. Where else may anyone
get that kind of information in such a perfect approach of writing?
I've a presentation next week, and I'm on the search for
such info.
We're having coffee at Nylon Coffee Roasters on Everton Park in Singapore.
I'm having black coffee, he's possessing a cappuccino.
He or she is handsome. Brown hair slicked back, glasses which fit
his face, hazel eyes and the most beautiful lips I've seen.
He or she is well developed, with incredible arms and also a chest that is
different during this sweater. We're standing
in front of each other talking about our way of life, what you want into the future, what we're looking for on another person. He starts saying that
they have been rejected a great deal of times.
‘Why Andrew? You're so handsome. I'd never reject you ', I say He smiles at me, biting
his lip.
‘Oh, I would not know. Everything happens for a
reason right. But tell me, you wouldn't reject me, might you Ana?' He said.
‘No, how could I?' , I replied
"So, utilize mind if I kissed you at the moment?' he explained as I am nearer to him and kiss him.
‘Next occasion don't ask, function it.' I reply.
‘I like how you would think.' , he said.
For the time being, I start scrubbing my high heel in their leg, massaging it slowly. ‘So what can you enjoy ladies? And, Andrew, don't spare me the details.' I ask.
‘I enjoy determined women. Someone you will never know whatever they want. A person that won't say yes simply because I said yes. Someone who's not scared when attemping interesting things,' he says. ‘I'm never afraid when you attempt something mroe challenging, especially with regards to making something mroe challenging in the sack ', I intimate ‘And I enjoy women who are direct, who cut through the chase, like you simply did. For being
honest, what a huge turn on.
amazing content thanks
amazing content thanks
This blog is amazing! Thank you.
thanks considerably this site will be proper plus everyday
Hello, Neat post. There is a problem with your site in internet explorer, could test
this? IE nonetheless is the market leader and a good component
to other folks will leave out your excellent writing due
to this problem.
Very good information. Lucky me I found your site by accident
(stumbleupon). I have bookmarked it for later!
Have you ever thought about writing an ebook or guest authoring on other sites?
I have a blog based on the same topics you discuss
and would love to have you share some stories/information. I know my audience would enjoy your work.
If you're even remotely interested, feel free to shoot
me an email.
Have you ever thought about writing an ebook or guest authoring on other sites?
I have a blog based on the same topics you discuss
and would love to have you share some stories/information. I know my audience would enjoy your work.
If you're even remotely interested, feel free to shoot
me an email.
If you are going for most excellent contents like myself, only visit this web site all the time since it presents feature
contents, thanks
Very good post. I am going through many of these issues as well..
Hello there, There's no doubt that your website may be having internet browser compatibility
problems. Whenever I take a look at your site in Safari, it looks fine however, when opening
in I.E., it's got some overlapping issues.
I merely wanted to provide you with a quick heads up!
Aside from that, excellent blog!
Hi there, I enjoy reading through your post.
I like to write a little comment to support you.
Hello, I enjoy reading all of your article post.
I like to write a little comment to support you.
Tremendous issues here. I'm very glad to look your post.
Thanks so much and I'm looking ahead to touch you.
Will you please drop me a e-mail?
You made some decent factors there. I appeared on the internet for the issue and found most people will associate with with your website.
These are in fact enormous ideas in concerning blogging.
You have touched some fastidious things here. Any way
keep up wrinting.
Right now it looks like Expression Engine is the top blogging platform out there right now.
(from what I've read) Is that what you are using on your blog?
Only wanna tell that this is extremely helpful, Thanks for taking your time to write this.
Amazing blog layout here. Was it hard creating a nice looking website like this?
When I initially commented I clicked the "Notify me when new comments are added" checkbox
and now each time a comment is added I get several emails with the same comment.
Is there any way you can remove me from that service? Cheers!
I have been exploring for a little for any high quality articles or weblog posts
in this kind of house . Exploring in Yahoo I eventually stumbled upon this
web site. Reading this info So i'm happy to exhibit that I have a very excellent uncanny feeling I came upon just what I needed.
I most indubitably will make sure to do not forget this web site and give it a glance on a relentless basis.
obviously like your web-site but you need to test the spelling on several of your posts.
Several of them are rife with spelling problems and I in finding it very bothersome to
inform the truth nevertheless I'll definitely come again again.
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
Hello there, I discovered your site via Google at the same time as searching for a related topic,
your website got here up, it seems great. I have bookmarked it in my google bookmarks.
Hi there, just became alert to your blog through Google, and
located that it's really informative. I am gonna watch out for brussels.
I'll be grateful if you happen to proceed this in future.
Lots of people will probably be benefited from your writing.
Cheers!
I visit everyday a few blogs and sites to read posts, except this
weblog gives feature based articles.
Greetings! This is my first comment here so I just wanted
to give a quick shout out and tell you I truly enjoy reading your blog posts.
Can you recommend any other blogs/websites/forums that deal
with the same topics? Thanks a ton!
thanks a lot this excellent website is actually conventional
plus everyday
Excellent article. Keep writing such kind of info on your
site. Im really impressed by your site.
Hello there, You've done an incredible job. I'll certainly digg it and personally suggest to my friends.
I'm confident they will be benefited from this web site.
Hi! Someone in my Myspace group shared this site with us so I came to check it out.
I'm definitely enjoying the information. I'm bookmarking and will be tweeting this to my followers!
Superb blog and brilliant design and style.
Woah! I'm really loving the template/theme of this blog.
It's simple, yet effective. A lot of times it's
difficult to get that "perfect balance" between user friendliness and appearance.
I must say you've done a excellent job with this. Also, the blog loads extremely fast for me on Opera.
Exceptional Blog!
It's going to be finish of mine day, but before end I am reading this fantastic piece of writing to increase
my know-how.
If some one desires to be updated with latest technologies then he must be pay a visit this web site and be up to date all the time.
stays on topic and states valid points. Thank you.
thank you web site admin
An outstanding share! I've just forwarded this onto a colleague who had been conducting a little research on this.
And he in fact bought me dinner because I discovered it for him…
lol. So let me reword this…. Thanks for the meal!! But yeah, thanks for spending some time to talk about
this issue here on your site.
thank you web site admin
Thanks for any other informative site. The place else
could I get that kind of information written in such an ideal manner?
I have a challenge that I am just now operating on,
and I've been on the glance out for such information.
Greetings! Very helpful advice within this article!
It is the little changes that will make the most significant changes.
Many thanks for sharing!
Amazing blog layout here. Was it hard creating a nice looking website like this?
Hi, I think your site might be having browser compatibility
issues. When I look at your blog site in Ie, it looks fine but when opening in Internet Explorer, it has some overlapping.
I just wanted to give you a quick heads up!
Other then that, great blog!
Hello, the whole thing is going well here and ofcourse every one is sharing information,
that's really fine, keep up writing.
How long does a copyright last on newspaper articles?. . If a service copies newspapers articles and then posts it in a database on the Internet, is there also a copyright on the Internet content?.
This piece of writing will help the internet viewers for creating
new blog or even a blog from start to end.
Fastidious answer back in return of this issue with firm arguments and telling all about that.
Keflex E Coli Susceptibility Viagra preisvergleich rezeptfrei Primatene Mist In Canada [url=http://ciali5mg.com]п»їcialis[/url] Canadian Pharmacy Meds Online Can I Take Sudafed With Amoxicillin On Sale On Line Provera Medication Cod Only
Date and Meet Single adult females in Brownsville
Brownsville was also a place for radical political causes during this time period. The Brownsville Recreation Center at the corner of Linden Boulevard, Mother Gaston blvd, And christopher Avenue. Marcus Garvey Houses further, Below Pitkin path, There is also a significant concentration of semi detached multi unit similar to those found in East New York and surrounding the public housing developments. The was a nominal state of Russia from 1570 to 1578 within, But did not actually gain self-sufficiency. for some individuals, It is an effective way to find love. Within many years of the first lot being distributed, had been 10,000 Jews basically Brownsville. in comparison, 38% of Brooklynites and 41% of city people have a college education or higher. It is all done for you really. a projected 25,000 customers lived in Brownsville by 1900, Most of whom lived in two story wooden frame hotels built [url=https://www.pinterest.com/asiameofficial/]asiame.Com[/url] for two families each. The third secondary school is Brownsville Academy, a Diploma Plus transfer school serving 10th through 12th grades with a 100% minority enrollment, EHarmony single men and women in Brownsville, TXAre you ready to join them and open up a new side of your sensuous moments? Meet Singles in Brownsville for fun and relationships It is not hard to start an online dating profile. by comparison, Brownsville is encompassed by other high poverty, High crime local neighborhoods like East New York, beach Hill, and therefore. Only 18% of the population have a college education or higher, But 28% have just one high school education and 53% are high school graduates with some college education. Zion Triangle The traffic triangle bounded by Pitkin and East New York Avenues and Legion Street was actually named Vanderveer Park after Peter L. all over 2004, The Chens sold the building to Family Services Network of New York, A funded by the local government. The Livonia Avenue motivation, A multi phase project based along Livonia Avenue, is supposed to create 791 apartments or houses for low income residents. Due to the area's high amount density, There are 39 public and charter schools serving elementary and junior high school students in Brownsville. working experience necessary, Brownsville is unlike similar neighborhoods in new york city that had since gentrified. Somers store, Which slopes gently down toward the southern Brooklyn shoreline. Weck is constantly on the record and produce in Memphis, In Ann Arbor at Lutz's Tazmania Studios and is the co driving force of the re united Brownsville Station. Brownsville used to be part of, But fundamental in 2012, a nearby became part of the. Brownsville is still majority black and Latino, With exactly two Jewish owned business organizations in Brownsville in 2012. Brownsville had not seen exactly the same revitalization because, different from Pico Union, It had not been encompassed by gentrified neighborhoods; Did not have sensible housing; And was not a historic district or an area of other relevancy. by 2015, Many community organizations had been formed to improve the well being in parts of Brownsville. Brownsville has profoundly higher in its schools. throughout the 2008, The represented the Betsy Head Play Center a landmark, Making it the first and only individual landmark in Brownsville. while using, The park honors Livonia and its native people, This also led to dangerous terminology; A 1935 collapse of a tenement stairway killed two people and injured 43 others. Just be honest and build a correct picture of yourself. He recorded a quantity of solo albums and toured with his own group The Points as well as blues man Hound Dog Taylor's backing band The Houserockers. Although a nearby was racially segregated, There were more attempts at improved total well being, open to the public mixing, And solidarity between black and Jewish neighbors than could be found in most other areas. by means 1935, various other land was added to the park including land purchased from the in 1928, which had built its New Lots Line in 1920. [url=https://issuu.com/asiame]aSiAme[/url] Start meeting singles in Brownsville and inhale the alluring scented of new love, a good idea emotions, And impressive memories.
Good day! I just want to offer you a big thumbs up for the excellent information you have got here on this
post. I'll be returning to your blog for more soon.
Hey very interesting blog! natalielise pof
What's up, of course this post is in fact
good and I have learned lot of things from it about blogging.
thanks.
I'm impressed, I have to admit. Seldom do I encounter a blog that's both educative and interesting, and let
me tell you, you have hit the nail on the
head. The issue is something which too few people are speaking intelligently about.
Now i'm very happy that I found this during my search for something regarding this.
I was very pleased to uncover this site. I want to to thank you for ones time for
this particularly wonderful read!! I definitely really liked every part of it and
i also have you book-marked to see new information in your website.
We are a group of volunteers and opening a new scheme in our community.
Your web site provided us with valuable info to work on. You've done a formidable job and our whole community will
be thankful to you.
Exceptional post however , I was wanting to know if you could write a litte more on this topic?
I'd be very thankful if you could elaborate a little bit further.
Many thanks!
Thank you for the good writeup. It in fact was once a enjoyment account it.
Look complex to far introduced agreeable from you!
However, how could we keep in touch?
Hello mates, its great article regarding
teachingand completely defined, keep it up all the time.
Hi! This is my first comment here so I just wanted to give a
quick shout out and tell you I genuinely enjoy reading through your articles.
Can you suggest any other blogs/websites/forums that deal with
the same subjects? Thank you so much!
I'm very pleased to uncover this page. I wanted to thank you for ones time for this particularly fantastic read!!
I definitely liked every little bit of it and I have you book-marked to look at new
stuff in your site.
I am usually to running a blog and i actually recognize your content. The article has really peaks my interest. I am going to bookmark your site and keep checking for new information.
I do not even know the way I finished up right here, but I believed this submit was once good.
I don't understand who you are but certainly you are going to
a famous blogger should you aren't already.
Cheers!
Hey there! I just wish to give you a big thumbs up for
the excellent information you've got here on this post.
I'll be coming back to your site for more soon.
If you are going for finest contents like I do, only go to see this web
page everyday because it provides feature contents,
thanks
It's an awesome post in support of all the online visitors; they
will take benefit from it I am sure.
Simply desire to say your article is as amazing. The clearness in your post is just spectacular
and i could assume you are an expert on this subject.
Well with your permission allow me to grab your RSS feed to keep up to date with forthcoming post.
Thanks a million and please keep up the gratifying work.
You made some respectable points there. I seemed on the web for the issue and found most people will go together with along with your website.
Somebody necessarily assist to make severely posts I would state.
This is the very first time I frequented your web page and up to now?
I surprised with the research you made to create this actual put up incredible.
Wonderful activity!
Deference to op , some superb selective information .
Hey! This is kind of off topic but I need
some advice from an established blog. Is it difficult to set up your own blog?
I'm not very techincal but I can figure things out pretty
fast. I'm thinking about creating my own but I'm
not sure where to begin. Do you have any
tips or suggestions? With thanks
Unquestionably believe that which you said.
Your favorite justification appeared to be on the internet the simplest thing to be
aware of. I say to you, I definitely get annoyed while people
think about worries that they plainly do not know about.
You managed to hit the nail upon the top and defined out the whole thing without having side effect , people could take a signal.
Will probably be back to get more. Thanks
I am 43 years old and a mother this helped me!
I am 43 years old and a mother this helped me!
I am 43 years old and a mother this helped me!
I am 43 years old and a mother this helped me!
I am 43 years old and a mother this helped me!
I was suggested this blog by my cousin. I'm not sure whether
this post is written by him as nobody else know such detailed about
my difficulty. You're wonderful! Thanks!
Excellent site you have here.. It's difficult to find excellent writing like yours nowadays.
I seriously appreciate individuals like you! Take care!!
I'm not sure why but this web site is loading incredibly slow for me.
Is anyone else having this issue or is it a problem on my
end? I'll check back later and see if the problem still exists.
I have read so many posts regarding the blogger lovers but this post
is actually a fastidious post, keep it up.
I needed to thank you for this excellent read!! I absolutely loved
every bit of it. I've got you book-marked to look at new things you post…
You've made some good points there. I looked on the internet for additional information about the issue and found most people will go along with
your views on this website.
Terrific article! That is the kind of info that should be shared around the net.
Disgrace on Google for now not positioning this post higher!
Come on over and visit my web site . Thank you =)
Do you mind if I quote a few of your articles as long as I provide credit and sources back to your site?
My blog is in the very same niche as yours and my visitors would truly benefit from
some of the information you provide here. Please let me know if
this okay with you. Regards!
Hey there just wanted to give you a quick heads up.
The words in your post seem to be running off the screen in Internet explorer.
I'm not sure if this is a format issue or something to do with web browser compatibility but I thought
I'd post to let you know. The design and style look
great though! Hope you get the problem resolved soon. Kudos
Hi there! It’s hard to find anything interesting on this subject (I mean something that is not overly simplistic), because everything related to 3D seems very difficult. You however seem like you know what you’re talking about :) Thank you for finding time to write relevant content for us!
Hi there colleagues, how is the whole thing, and what you wish for to say about this
piece of writing, in my view its in fact remarkable in favor of me.
stays on topic and states valid points. Thank you.
Keep on writing, great job!
Only wanna tell that this is extremely helpful, Thanks for taking your time to write this.
Hi there to every single one, it's really a pleasant for me to go to see this
web page, it consists of useful Information.
I just want to mention I’m all new to blogs and certainly savored you’re web site. More than likely I’m want to bookmark your site . You surely have good writings. Appreciate it for sharing your web page.
Amazing blog layout here. Was it hard creating a nice looking website like this?
Hi there to every one, the contents present at this web site are genuinely awesome
for people experience, well, keep up the good work fellows.
you're actually a excellent webmaster. The site loading
speed is amazing. It seems that you are doing any distinctive trick.
In addition, The contents are masterpiece.
you've performed a excellent process in this subject!
Thanks to my father who informed me on the topic of this website, this webpage is genuinely awesome.
thank you web site admin
My family every time say that I am wasting my time here at web, however
I know I am getting know-how all the time by reading thes fastidious articles or reviews.
I love what you guys are up too. Such clever work and coverage!
Keep up the very good works guys I've you guys to blogroll.
Have you ever thought about publishing an e-book or guest authoring on other websites?
I have a blog based on the same information you discuss and would love to
have you share some stories/information. I know my audience would enjoy your work.
If you are even remotely interested, feel free to
send me an email.
Hi! Quick question that's totally off topic.
Do you know how to make your site mobile
friendly? My website looks weird when viewing from my iphone.
I'm trying to find a theme or plugin that might be able
to correct this problem. If you have any suggestions, please share.
With thanks!
Respect to website author , some wonderful entropy.
What a material of un-ambiguity and preserveness of valuable familiarity about unexpected emotions.
DailyNewsGallery.Com – Get lates news – Breaking News, Top Video News, Education News, Tech News, Entertainment andsports News from here
Hi there! I just would like to give you a huge thumbs up for your great information you have got here on this post.
I am returning to your blog for more soon.
I was wondering if you ever thought of changing the
layout of your website? Its very well written; I love what youve got to
say. But maybe you could a little more in the way of content so people could
connect with it better. Youve got an awful lot of
text for only having 1 or 2 images. Maybe you could space
it out better?
With havin so much content and articles do you ever run into any issues of plagorism or
copyright infringement? My blog has a lot of exclusive content I've
either authored myself or outsourced but it appears a lot of
it is popping it up all over the web without my permission. Do you know any methods to help protect against content from being ripped
off? I'd genuinely appreciate it.
I every time emailed this webpage post page to all
my contacts, for the reason that if like to read it after that my friends will too.
natalielise pof
SSC Result – Check Bangladesh education board exam result SSC Result 2020
I like the valuable information you provide in your articles.
I'll bookmark your blog and check again here frequently.
I'm quite sure I will learn many new stuff right here! Good
luck for the next!
The other day, while I was at work, my sister stole my apple ipad and tested to see if it can survive
a 30 foot drop, just so she can be a youtube sensation. My iPad
is now destroyed and she has 83 views. I know this is completely off topic but I had to share it
with someone!
Hello! I could have sworn I've visited this web site before but after browsing
through many of the posts I realized it's new to me.
Nonetheless, I'm definitely delighted I found it and I'll be book-marking it and checking back frequently!
Great post. I used to be checking constantly this blog and I'm impressed!
Very helpful information specifically the final section :) I take care of such information much.
I used to be looking for this certain information for a very long time.
Thank you and good luck.
It's fantastic that you are getting ideas from this paragraph as well as from our argument made at this time.
What's up, everything is going sound here and ofcourse
every one is sharing information, that's really fine, keep up
writing.
You made some really good points there. I looked on the web for more info about the issue and found most individuals will
go along with your views on this web site.
I must say got into this site. I found it to be interesting and loaded with unique points of interest.
Very great post. I just stumbled upon your blog and wished
to mention that I've really enjoyed browsing your blog
posts. In any case I will be subscribing to your feed and I hope you write once more very soon!
Excellent blog you have here but I was wondering if you knew of any
discussion boards that cover the same topics talked about here?
I'd really like to be a part of community where I can get feedback from other
knowledgeable people that share the same interest.
If you have any recommendations, please let me know.
Thanks!
Hey there! I've been following your website for some time now and finally got the courage to go ahead and give you a shout out from
Huffman Tx! Just wanted to mention keep up the
excellent work!
I'm gone to inform my little brother, that he should also pay a visit this weblog on regular
basis to obtain updated from most recent gossip.
Aw, this was a really nice post. Taking the time and actual effort to create a top notch article…
but what can I say… I hesitate a whole lot and never manage to
get nearly anything done.
This website was… how do I say it? Relevant!!
Finally I have found something that helped me. Kudos!
Good day! Would you mind if I share your blog with my myspace group?
There's a lot of folks that I think would really appreciate your content.
Please let me know. Many thanks
Excellent blog you have here but I was wanting to know if you
knew of any user discussion forums that cover the
same topics talked about in this article? I'd really love to be a part of group
where I can get responses from other experienced people that share the same interest.
If you have any suggestions, please let me know. Bless you!
This information is invaluable. How can I find out more?
Good answers in return of this matter with real arguments and explaining the whole thing
concerning that.
I really like what you guys tend to be up too. This kind of clever work
and exposure! Keep up the awesome works guys I've added you guys to our blogroll.
Hi there! I know this is somewhat off topic but
I was wondering if you knew where I could find a captcha plugin for
my comment form? I'm using the same blog platform as yours
and I'm having trouble finding one? Thanks a
lot!
Magnificent goods from you, man. I've understand your
stuff previous to and you are just too wonderful. I
actually like what you've acquired here, really like what you are saying and the
way in which you say it. You make it enjoyable and you
still care for to keep it smart. I can't wait to read far more from
you. This is actually a wonderful site.
Hello there! I just wish to offer you a huge thumbs up
for your great information you have right here on this post.
I will be coming back to your website for more soon.
Very nice article, totally what I needed.
Wow, this paragraph is nice, my younger sister is analyzing these things, so I am going to let know her.
Hello, i just want to thank you for your excellent article. Keep it well.
Really preciate you for your information you provide. I have tried a lot but couldn’t find it.Thank you.
I were caught in same trouble too, your solution really good and fast than mine. Thank you.
Hard to ignore such an amazing article like this. You really amazed me with your writing talent. Thank for you shared again.
I appreciate your Post you are Given me Right Information about Survey Result so Thanks for this Post.
Amazing blog, get the mutual fund schemes offered by Investment Firms & best Mutual Fund Companies.
Toko Otomotif : alat teknik, perkakas bengkel, alat safety, alat ukur, mesin perkakas, scanner mobil, alat servis motor, alat cuci mobil, mesin las.
Thank you for posting such a great blog.
Wow!!! It was really an Informational Article which provide me with much Insightful Information. I would like to first thank the author for such an Insightful Content. If someone here is looking for a Website Designing Company in India, then look no further than Jeewangarg.com as we are the best Website Designing Company in Delhi working in the arena for the last 8 years.
I have been a keen follower of your website.
recently I came across this topic and after reading the whole article I am amazed that how well you have written it.
Amazing writing skills shown.
You have done a good research on this topic.
Great Work.
Great post! I really enjoyed reading it. Keep sharing such articles. Looking forward to learn more from you.
If you are looking for the best thesis editing and proofreading services provider in Singapore then you must get in touch with the Singapore experts team. Translation services Singapore is the most genuine translation services provider in Singapore and across the globe. We offer to specialize thesis editing services for scholar and postgraduate students.
For best thesis writing help in New Zealand. NZ Assignment help is the best option. Our writers are providing many of the assignment help services for all college and university students studied in New Zealand. We are providing our services in Auckland and Hamilton.
For best research paper writing help in UAE. UAE Assignment help is the best place. Our writers are highly qualified and they are working from past 10 years in assignment writing services. We have secured payment option so your money is in safe hand.
When it comes to makeup, Shweta Gaur is the name that comes in mind of thousands of people who are looking for a reliable and professional makeup artist. SGMA Salon & Academy PVT LTD was established in 2014 and is owned by Shweta Gaur, a celebrity Makeup Artist, and fashion expert renowned not only in India but worldwide. SGMA offers both full time and part-time courses leading to lucrative career opportunities. With a passion to provide quality makeup education and after 8 years of successful operation, the SGMA Salon & Academy PVT LTD has expanded its branches in Delhi/NCR & Bengaluru.
Decent, What an Excellent post. I truly discovered this an excessive amount of data. It is the thing that I was looking for. I might want to propose you that please continue sharing such sort of information. Much appreciated
This is a very great post and the way you express your all post details that is too good.thanks for sharing with us this useful post..