Making data races manifest themselves

Or, synchronization, valgrind and poset dimension.

This story is perhaps more technical than I ever allowed myself to get online. If I may say so – it may be worth following; I can say that it really changed my perspective on what data races are.

I'll need to explain a bit about the context:

• how we structure our parallel apps for multi-core targets
• how we catch synchronization bugs using a custom valgrind tool
• which of the bugs were hard to catch that way

Then I can explain how we now catch them all (at least those having any chance to happen on our test inputs; you'll see what I mean).

I'll also discuss valgrind's standard race detection tool, helgrind. I'll try to show that the interface to parallelism it works against – pthreads – poses a much harder problem, and how races can go undetected because of that.

I hope this can be interesting outside of my specific work context because "catching all the races" seems to be a claim rarely made. Also we got to stumble upon a well-known math problem during mundane pointer-chasing – a cliche of sorts, but amusing when it actually happens.

So, here goes.

Our parallelism framework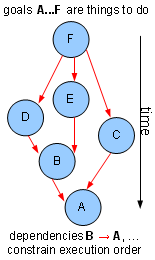

…known in its current incarnation as GSF – "Goal/Graph Scheduling Framework". It's fairly simple – 4 paragraphs and 2 pseudo-code listings should be a reasonable introduction.

The idea is, your app is a graph of goals. The nodes, goals, are things to do – typically function pointers (could be function objects or closures). The edges are dependencies – A depends on B, so A must be executed after B (denoted with B → A in the diagrams). The main loop does this:

goal = first_goal # a dummy everything depends on
while goal != last_goal: # a dummy, depends on everything
  update_dependent_goals_status(goal) # find READY goals
  for chosen in sched.choose_goals(): # scheduler
    chosen.resource.enqueue(chosen) # outgoing message Qs
  goal = dequeue_finished_goal() # incoming message Q

This runs all the goals in a graph, and can itself be invoked in a loop – in our case, we run all the goals for every grabbed video frame.

Whatever the scheduling policy, a correct execution order will be chosen. Only READY goals can run, and a goal only becomes READY when everything it depends on becomes DONE. This is implemented in update_dependent_goals_status:

goal.status = DONE
for dep in goal.dependent_goals:
  dep.num_predecessors -= 1
  if dep.num_predecessors == 0:
    dep.status = READY

The scheduling policy is implemented partly in sched.choose_goals – the scheduler, and partly in resource.enqueue – the queues. The scheduler decides who is enqueued first; some queues may reorder waiting goals by priority, or even suspend the running goal(s) when a more important one arrives. While the scheduling policy can be made complicated almost without bound, that's all there is to the framework itself.

To summarize in standard terms, it's a kind of a message passing framework, without explicit threads and without locking, but with (massive) data sharing. "Goal scheduled"/"goal finished" notifications are the only messages, and only used by the framework – the goals themselves always communicate through shared data. Dependencies are the only synchronization primitive. OS locks are never used, except in the guts of various memory allocators.

Drawbacks

Users, or "application programmers", usually hate this framework with a passion, because code is hard to read and modify.

To break your app into the sort of graph described above, you need to specify the goals and the dependencies. Currently we do both in ugly ways. Goals are specified as global functions, with context passed through global variables: void goal_A() { g_ctxt… }. The hairy dependency graph is constructed by a Python script running at build time, with ifs, loops, and function calls – if do_A: make_goal("A",dep="B C"). This adds ugliness to C++ code, and then makes you follow ugly Python code to figure out the execution order of the ugly C++ code.

Some of it was even uglier in the past. Some of it could become less ugly in the future. At least one serious limitation is irremediable – the inability to create goals at run time. For example, you can't say "create a goal per processed data item" – rather, you need to explicitly, statically create a goal per CPU and distribute the data between the goals. You can't say "if X happens, create that goal" – you need to always have that goal, and have it do nothing unless X happens. People don't like to look at their flow that way.

Motivation

Efficiency and correctness, basically. Efficiency is tangential to our story, so I won't discuss it (and frankly, we aren't sure how much efficiency we gain, compared to other approaches). As to correctness – the hateful thing indeed "scales", which is to say, it doesn't break down. We've managed to ship working code for several years, given:

• 8 to 10 heterogeneous target cores
• Hundreds of goals
• Dozens of applications
• Dozens of developers

…the worst thing being "dozens of developers" – most unaware of parallelism, as I think they should be. Not that it proves we couldn't have done it differently – I can only give my theory as to why it would be harder.

The biggest problem with parallel imperative programs is synchronizing access to shared data. Tasks/threads can, and are encouraged to communicate through messages, but eliminating sharing is hard:

• People frequently don't even realize they're sharing data

• If tools make implicit use of shared data impossible, things can get painful (think of explicitly passing around a particularly "popular" data item, or copying large/intertwined objects)

Sharing data is natural and efficient in imperative programs, and outlawing it is hard. And locks are problematic since

• You can have deadlocks, and
• You can forget to lock.

Now, if you schedule a statically known flow graph rather than an unconstrained threaded app, it turns out that you solve both of these problems:

• Deadlocks are trivially prevented - at build time, check that the dependency graph has no cycles

• Undeclared dependencies – sharing data without proper synchronization – can be found using program instrumentation

Our subject is this second bit – using program instrumentation to find race conditions (which makes everything up to this point an unusually long introduction).

We use a custom valgrind plug-in ("tool" as they call it) for program instrumentation. It works somewhat similarly to valgrind's helgrind tool, though helgrind's implementation is much more complicated.

However, helgrind has false negatives – it will consistently miss some of the data races, as I believe will any tool lacking the knowledge of the overall app structure. A simple example of a data race unreported by helgrind appears after the discussion on race condition detection, when the problem should become more clear.

Race conditions in a static graph

In an imperative program, goals communicate through memory. A memory access can thus be thought of as a proof of dependence. If goal A accesses memory at address X, and goal B was the last to modify X, then A depends on B. If there is no path from A to B in the dependency graph, the program is buggy. A could run before B or after it, so the result of accessing X is undefined.

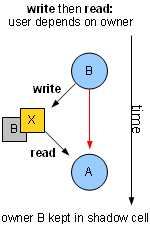
Suppose we could intercept all load/store instructions in the program. Then we could maintain, for every byte, its current "owner" – a goal ID. A store to a location would update its owner to the ID of the currently running goal. Loads and stores could then check whether the currently running goal depends on the owner of the accessed location – all it takes is accessing a 2D array, the path matrix. Upon error, print the call stack, and the names of the 2 goals.

This sort of thing is surprisingly easy to implement on top of valgrind, almost as easy as implementing an interface with abstract onLoad and onStore methods. I thought of posting sample code but it looks like the example tool shipped with valgrind, "lackey", comes with a load/store interception example these days.

As to the "shadow memory" you need for keeping owner IDs – you can do that with a page table, along the lines of a virtual memory implementation in an OS. The high bits of a pointer select a page and the low bits are the offset within the page, with pages allocated upon first access. Standard valgrind tools do it this way, too.

Our valgrind tool is called shmemcheck for "shared memory checker". A lame pun on memcheck, valgrind's most famous tool, the one reporting uninitialized memory access. "Memcheck-shmemcheck". Probably the last time I used this sort of name – funny for the first few times, embarrassing for the next few thousands of times.

Despite the embarrassment, when we got an implementation good enough to be systematically used, it was really great – data races were decimated. Valgrind is awesome, unbelievably so. It managed to unimaginably expand what can be done to a natively compiled program, decades after the tools for building native programs were cast in stone.

The trouble with this version of, cough, shmemcheck, is that it doesn't really work. That is, sometimes you have false negatives, so you still get to dive into core dumps. Why?

What about the opposite case?

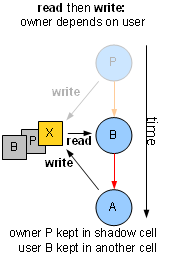If A loads from X that was last modified by B, A depends on B, and we detect it alright. What if A writes to X that was previously read by B? This also proves that A should depend on B. Otherwise B will sometimes run after A, reading its update to X, and sometimes before A, reading the previous value. In order to detect this dependency, we have to remember that X was read by B until A stores to X.

…What if, in addition to B, X was read by C, D, and E, all before A's update?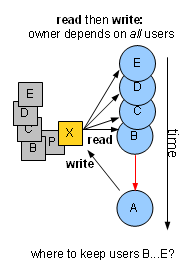

Every location always has one "owner" but can have many "users". We can afford keeping an ID – 2 bytes in our case – for every byte. Keeping – and checking – a list of users that could grow to tens or even hundreds of IDs per location sounds impractical.

We used all sorts of application-specific arguments to convince ourselves that this problem is confined to a few particular scenarios. We had a few hacks removing some of the false negatives, at the cost of adding some false positives, and lived with that.

Choosing the order

We got used to think that the question was, how do you know who reads X before A? But then it dawned upon us that the right question was: why do they read X before A?!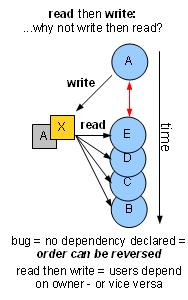

And really – if B, C and D run before A because it is stated in the dependency graph that A depends on B, C and D – then there's no bug to worry about. But if there's no dependency declared between, say, A and B, then A could run before B just as well – and we'd detect the bug. So we only missed the race condition because of a randomly chosen order. And when we do find races, we don't know if B depends on A or vice versa – only that we were lucky to have A run first.

What if we choose different random orders and run the same app many times? Then in some run, A will run before B and we'll find the bug – with just one shadow cell keeping the owner.

…Or will it? We have in our dependency graph many "A, B" pairs of independent goals. If we pick random orders, how likely are these pairs to "flip" to "B, A" in some orders but not others?

The first conjecture was – very likely. Just randomize schedules by having sched.choose_goals pick a random goal among the READY ones. "There seems to be no bias in the selection; A and B are independent so the chance for A to come before B is 1/2; therefore, with N orders, the chance for A to always follow B is 1/2^N – small enough."

Interestingly, it still sounds reasonable to me, though I found a counter-example, just out of fear that it's too good to be true (what, years of core dumps are now behind me?) The counter example is, suppose you have two long processes, P and Q, each made up of 100 goals, P1…P100 and Q1…Q100. P and Q are declared independent – Pi never depends on Qj or vice versa. However, Pi+1 depends on Pi, similarly for Q, so P and Q goals can run in just one order.

Just two schedules would "flip" all independent pairs: (1) Run P, then Q and (2) Run Q, then P. However, sched.choose_goals has a snowflake's chance in hell to pick these schedules. The set of READY goals will contain, at all times, 2 goals: one from P and one from Q. sched.choose_goals must either choose the one from P 100 times in a row, or the one from Q 100 times in a row. Since that's a 1 in a 2^100 event, P1 will always run before Q100. If P1 loads from X and Q100 stores to X, we'll never find the undeclared dependency.

One could say that things that aren't likely to flip in such random trials are unlikely to flip in reality and it'd be 100% wrong. In reality, execution order depends on real run times and those create a very biased, and an unpredictably biased sampling of the distribution of schedules.

Now, with N goals, N*2 orders would clearly be enough to flip all pairs – for every goal, create an order where it preceeds everything it doesn't depend on, and another order where it follows everything it doesn't depend on. But our N is above 1000, so N*2, though not entirely impractical, is a bit too much.

Poset dimension

Our pessimism resulting from the collapse of the first conjecture lead to an outburst of optimism yielding a second conjecture – just 2 orders are enough to flip all pairs. Specifically, the orders we thought of were a DFS postorder and its "reversal", where you reverse the order in which you traverse the children of nodes.

Works on my P & Q example indeed, but there's still a counter-example, just a bit more elaborate. We kept looking at it until it turned out that we shouldn't. The dependency graph makes the goals a partially ordered set or poset. Finding the minimal number of schedules needed to flip all independent pairs would find the order dimension of that poset. Which is a known problem, and, like all the good things in life, is NP-hard.

Curious as this discovery was, I was crushed by this NP-hardship. However, there still could be a good practical heuristic yielding a reasonably small number of orders.

We tried a straightforward one – along the lines of the N*2 upper bound, "flip them one by one", but greedier. Simply try to flip as many pairs as you can in the same schedule:

1. Start with a random schedule, and make a list of all the pairs that can be flipped.
2. Starting with the real dependencies, add fake dependencies forcing pairs from the list to flip, until you can't add any more without creating a cycle.
3. Create a schedule given those extended dependencies.
4. Remove the pairs you flipped from the list. If it isn't empty, go to step 2.

This tended to produce only about 10 schedules for more than 1000 goals, and there was much rejoicing.

Massive testing

Instrumentation slows things down plenty, so you can't run many tests. This is a pity because instrumentation only catches data races that actually occurred – it's actual loads by A from location X owned by B that prove that A depends on B. But if you can't run the program on a lot of data, you may not reach the flow path in A that uses X.

However, if you can, with just 10 schedules, flip all "A, B" pairs, you don't need instrumentation in the first place. Just run the app with different orders on the same data, see if you get the same results. If you don't, there's a race condition – then run under instrumentation to have it pin-pointed to you. The order is "purposefully diversified", but deterministic, so problems will reproduce in the second, instrumented run. Thus massive runs can be uninstrumented, and therefore, more massive.

So not only does this cheap poset dimension upper bound business solve the false negatives problem with instrumentation – it also greatly increases coverage. Of course there can still be a race that never occurred in any test runs. But now the quality of testing is defined just by the quality of the test data, never by chance. With races, whether you detect them or not is thought of as something inherently having to do with chance. It turns out that it doesn't have to.

Helgrind's problem

Helgrind – or any tool lacking knowledge about the app structure – can not meaningfully reorder things this way, in order to "make races manifest themselves". A race can be detected if A that stores to X is moved to happen before B that loads from X, but in order to do that, you have to know where A and B are.

Helgrind's only markers breaking the app into meaningful parts are synchronization calls, like mutex locks/unlocks. But it doesn't know where they'll happen in advance. So it can't stir the execution so that "this lock happens as early as possible" – there's no "this lock" until a lock actually happens. By then it's too late to make it happen before anything else that already happened. (In theory, the app structure could be inferred dynamically from the flow, I just don't see how I'd go about it.)

Therefore, helgrind seems to have the same problem our first versions of shmemcheck had. You can keep the single owner of a location but not its many readers; it appears that helgrind keeps one reader – the last. Helgrind's "owner/reader" is a lock ID rather than a goal ID, but I think the principle is very similar.  I haven't studied helgrind's interals so I only speculate about how it works, but I easily managed to create an example where it gives a false negative:

1. In thread A, read X without locking, as many times as you want (…or don't want – in a real program it would be a bug, not an achievement…)
2. After that, read X once with proper locking.
3. In thread B, modify X, again with proper locking.

If, during testing, thread B happens to modify X after all of thread A's reads from X, the bug in A – unsynchronized access to X – will go unnoticed. It won't go unnoticed if thread A never locks properly – since helgrind will remember and report the last of its unsynchronized reads:

#include <pthread.h>
#include <stdio.h>

pthread_mutex_t mutex = PTHREAD_MUTEX_INITIALIZER;
int shared=1;
int unused=0;
typedef struct { int read_unlocked, read_locked; } sopt;

void* child_fn(void* arg) {
  sopt* opt = (sopt*)arg;
  if(opt->read_unlocked) {
    unused += shared;
  }
  if(opt->read_locked) {
    pthread_mutex_lock(&mutex);
    unused += shared;
    pthread_mutex_unlock(&mutex);
  }
  return 0;
}

void testhelgrind(int read_unlocked, int read_locked,
                   const char* expected) {
  fprintf(stderr,"expected behavior: %sn", expected);
  //fork
  sopt opt = { read_unlocked, read_locked };
  pthread_t child;
  pthread_create(&child, 0, child_fn, &opt);
  //lock & modify shared data
  pthread_mutex_lock(&mutex);
  shared = 2;
  pthread_mutex_unlock(&mutex);
  //join
  pthread_join(child, 0);
}

int main(void) {
 testhelgrind(0,1,"no errors reported [true negative]");
 testhelgrind(1,0,"data race reported [true positive]");
 testhelgrind(1,1,"no errors reported [false negative]");
}

Which, under valgrind –tool=helgrind, prints:

expected behavior: no errors reported [true negative]
expected behavior: data race reported [true positive]

...
==15041== Possible data race during write of size 4 at 0x804a024 by thread #1
==15041==    at 0x8048613: test_helgrind (helgrind_example.c:33)
==15041==    by 0x8048686: main (helgrind_example.c:41)
==15041==  This conflicts with a previous read of size 4 by thread #3
==15041==    at 0x804856E: child_fn (helgrind_example.c:14)
...

expected behavior: no errors reported [false negative]

…or at least it works that way on my system, where the child thread runs first.

So if helgrind does report a data race – be sure to look careful. If you have several buggy reads, and only fix the last one and run again, helgrind will very likely not report the previous one. Your new synchronization code around the last read now "masks" the previous read.

The happy ending

We still have false negatives in our data race detection, but these are just easy-to-fix low-level loose ends – or so I think/hope. Things like tracking memory writes by devices other than CPUs, or handling custom memory allocators. I'm looking forward to have these false negatives eliminated, very sincerely. Few things are uglier than debugging data races.

I never thought this through enough to tell whether this purposeful reordering business can be utilized by a framework more restrictive than "use raw threads & locks", but less restrictive than "your app is a static graph". If it can be (is already?) utilized elsewhere, I'd be very curious to know.

Special thanks to Yonatan Bilu for his help with the math.